Расчет системы автоматической стабилизации заданного значения выходной координаты (расчетно-графическое задание), страница 4

При , в рассматриваемой САР обеспечивается требуемая точность стабилизации выходной координаты в установившемся режиме.

4  Анализ устойчивости исходной САР

4.1  Устойчивость по критерию Гурвица

Используя формулу (2.12) или (2.14) можно записать характеристическое уравнение замкнутой системы:

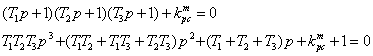
Запишем характеристическое уравнение в общем виде:

                        ,                           (4.1)

где 

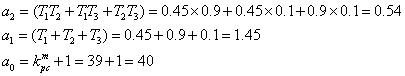
Запишем главный определитель Гурвица

        

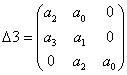
Теперь необходимо проверить выполняются ли условия критерия Гурвица:

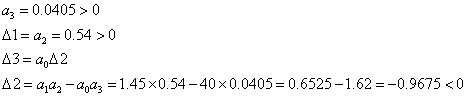
Поскольку , а следовательно и , то в соответствии с критерием Гурвица исходная САР является неустойчивой.

Исходная САР находится на границе устойчивости при условии:

                                                                                   (4.2)

Поскольку >0 , то можно записать:

       ,

отсюда можно найти граничное значение коэффициента передачи разомкнутой системы:

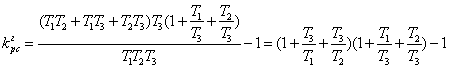                               (4.3)

Подставив в (4.3) значения, получим:

                     

Таким образом, для исходной САР верно неравенство:

                                                                                                    (4.4)

4.2  Устойчивость по критерию Найквиста

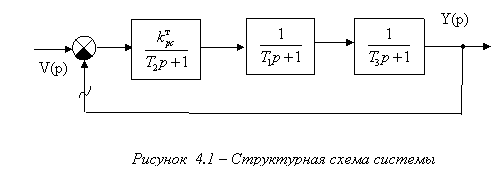
Условием применения критерия является необходимость приведения исходной структурной схемы к одноконтурной. При этом следует учитывать соотношение между постоянными времени (). Преобразованная структурная схема приведена на рисунке 4.1.

  

Для звена с передаточной функцией W₁(p) можно рассчитать логарифмические частотные характеристики:  

                        дБ

                      

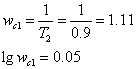
Для звена с передаточной функцией W₂(p) можно рассчитать логарифмические частотные характеристики:  

                        дБ

                    

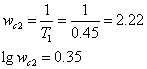
Для звена с передаточной функцией W₃(p) можно рассчитать логарифмические частотные характеристики:  

                       дБ

                   

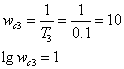
На рисунке 4.2 представлена логарифмическая частотная характеристика исходной системы.  В соответствии с рисунком можно определить запас устойчивости по фазе по формуле: .

Поскольку , то в соответствии с критерием Найквиста исходная САР является неустойчивой.

5  Коррекция динамических свойств системы

5.1  Расчет корректирующего устройства