Расчет системы автоматической стабилизации заданного значения выходной координаты (расчетно-графическое задание), страница 3

Y(p) = W_з ^в(p)F(p)                                    (2.15)

В соответствии с принципом суперпозиции на основе формул (2.12) – (2.15) можно записать расчетную формулу изображения Лапласа выходного сигнала:

     (2.16)

3  Статический расчет

1)  Исходная система в разомкнутом состоянии

При этом не требуется измерение выходной регулируемой координаты y

Используя теорему о предельных значениях на основе формулы (2.16) в установившемся режиме можно записать:

                   

              

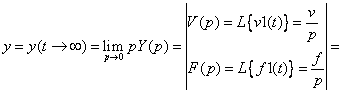
Тогда уравнение статики разомкнутой системы имеет вид:

                             ,                             (3.1)

где   - заданное значение выходной регулируемой координаты системы,

 - величина, на которую уменьшается  выходная координата системы под      действием возмущения.

Пусть и , а  (максимальное возмущающее воздействие, исходя из исходных данных). Следовательно,

Поскольку выполняется условие                          ,                 (3.2)

где     - требуемая точность стабилизации системы в статическом режиме (из   исходных данных).

Разомкнутая система должна быть заменена замкнутой системой автоматической стабилизации заданного значения выходной координаты.

2)  Исходная система в замкнутом состоянии

На основе формулы (2.16) аналогично можно записать уравнение статики замкнутой системы:

 

Уравнение статики замкнутой системы:

                                    ,                 (3.2)

где   - заданное значение выходной регулируемой координаты системы,

 - величина, на которую уменьшается  выходная координата системы под      действием возмущения.

В соответствии с заданием на проектирование можно записать  или:

                                                                                 (3.3)

Заменив в (3.3) неравенство на равенство можем окончательно записать:

                                                                                     (3.4)

Требуемое значение коэффициента передачи разомкнутой системы рассчитывается по формуле:

                                                                                   (3.5)

Подставив исходные значения, получим:          .

Так как , то требуемое значение коэффициента передачи решающего блока рассчитывается следующим образом:

                                                                                  (3.6)

Подставив значения, получим   .