Здесь A – это BrO3–, X – HBrO2, Y – Br–, Z – M(n+1)+, P, Q – продукты реакции. Реакция (O1) орегонатора соответствует реакции (R3) механизма ФКН, (O2) – (R3), (O3) – (R5), (O4) – (R4), а (O5) – процессу C. Ценность орегонатора заключается в том, что его можно исследовать аналитически, и он успешно моделирует реакцию БЖ.
Кинетические уравнения, описывающие изменение концен-траций автокатализатора (X = HBrO2), бромид-иона (Y = Br–) и катализатора (Z = M(n+1)+), выглядят следующим образом [5]:
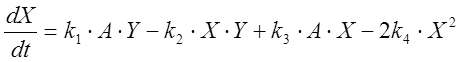 ;
(1)
;
(1)
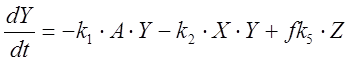 ; (2)
; (2)
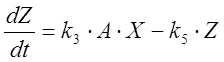 . (3)
. (3)
Обычно при записи этих уравнений используют
безразмерные переменные ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
которые связаны с концентрациями соединений X, Y, Z, A
и константами скоростей
,
которые связаны с концентрациями соединений X, Y, Z, A
и константами скоростей ![]() –
– ![]() следующим образом:
следующим образом:
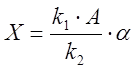 ,
, 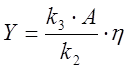 ,
, 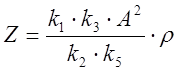 ,
, 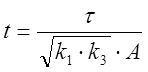 ,
, 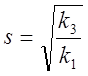 ,
, 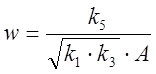 ,
, 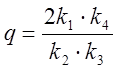 .
.
Тогда уравнения (1–3) перепишутся в виде [14]
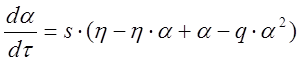 ; (4)
; (4)
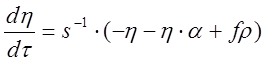 ; (5)
; (5)
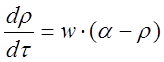 . (6)
. (6)
Математический анализ уравнений (4–6) в целях
обнаружения колебательных решений впервые был проведен Филдом и Нойесом [16] и
показал, что при любом ![]() > 0 имеется единственное
стационарное решение
> 0 имеется единственное
стационарное решение
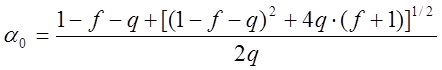 ; (7)
; (7)
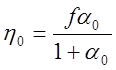 ; (8)
; (8)
![]() . (9)
. (9)
Для нахождения колебательных решений нужно определить собственные числа матрицы:
|
½ ½ ½ |
s× (1–2q×X0 – Y0) |
s× (1 – X0) |
0 |
½ ½. ½ |
|
|
– Y0 / s |
– (1 + X0) / s |
f / s |
(10) |
||
|
w |
0 |
– w |
Если все три собственных числа данной матрицы имеют
отрицательные действительные части, то малое возмущение стационарного состояния
будет затухать и система вернется в состояние покоя. Однако если хотя бы одно
из собственных чисел будет иметь положительную действительную часть, малые
возмущения начнут нарастать, при этом возможно появление колебаний. Филд и
Нойес [16] провели полный численный анализ поведения собственных чисел данной
матрицы в зависимости от параметров ![]() и
и ![]() и определили области устойчивости и
неустойчивости модели Орегонатор.
и определили области устойчивости и
неустойчивости модели Орегонатор.
Еще одна химическая реакция, в которой экспериментально наблюдали колебания концентраций реагентов, интермедиатов и продуктов – осциллирующая реакция Брея–Либавского (БЛ). Известно, что в кислой среде пероксид водорода термодинамически способен окислить I2 до IO3– и восстановить IO3– до I2:
5 H2O2 + 2 IO3– + 2 H+ ¾® I2 + 5 O2 + 6 H2O; (А)
5 H2O2 + I2 ¾® 2 IO3– + 2 H+ + 4 H2O. (В)
В 1921 г. Брей [17] решил, что IO3– должен быть идеальным катализатором разложения Н2О2:
2 H2O2 ¾® 2 H2O + O2. (C)
При проведении этой реакции при 50 ºС в очень узком диапазоне значений pH и концентраций реактантов он наблюдал колебания. Механизм данной реакции также включает автокаталитическую стадию, а автокатализатором является HIO2 [16].
Авторы [17] открыли, что добавление малоновой кислоты и Ce(III) или Mn(II) к системе БЛ ведет к чрезвычайной интенсификации колебаний концентраций I2, I–, I3–, O2, CO2. Если в реакционную среду также добавить крахмал, цвет раствора будет меняться от бесцветного к желтому и синему по циклу.
Окисление углеводородов и других веществ в газовой фазе также может происходить колебательным образом. Колебания сопровождаются импульсами света и ростом температуры по меньшей мере на 200 ºС. К неустойчивому состоянию и колебаниям может вести цепной механизм этих реакций. Однако в газофазных системах существует и другой механизм возникновения неустойчивого состояния. Из-за низкой плотности газов и как следствие их плохой теплопроводности даже небольшая экзотермичность реакции может вести к значительному росту температуры и возникновению обратной связи в результате температурной зависимости констант скорости реакции. Эти тепловые эффекты могут вести к так называемым термокинетическим колебаниям [14].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.