Пусть ![]() непрерывно
диф-мы в D. Тогда имеет место формула
непрерывно
диф-мы в D. Тогда имеет место формула 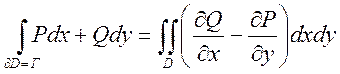
Доказательство:
Рассмотрим 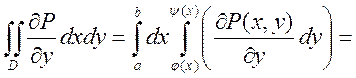 (по формуле Н-Л)=
(по формуле Н-Л)= 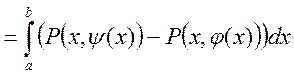

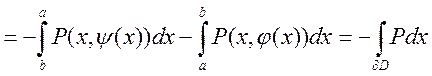 . Аналогично для Q.
. Аналогично для Q.
Формула Гаусса-Остроградского
Теорема:
Пусть функции P,Q,R –
непрерывно диф-мы в ![]() . Тогда имеет место формула:
. Тогда имеет место формула:  ,
,
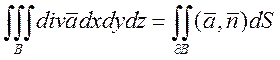
Доказательство:
Рассмотрим 
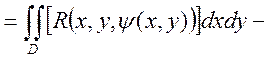
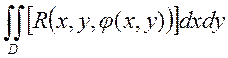
{![]() формула
формула ![]() }
}
…=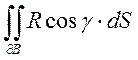
Поэтому 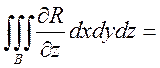
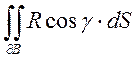 так и для P, Q
так и для P, Q
Формула Стокса
Теорема
Если вектор ![]() является непрерывно диф-мой, то имеет
место равенство
является непрерывно диф-мой, то имеет
место равенство  , {
, {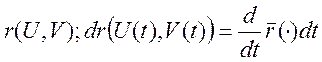 -
покомпонентно}
-
покомпонентно}
Доказательство: иначе формулу
записывают 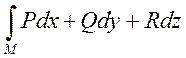 . Край определяется так: берутся
. Край определяется так: берутся ![]() и
и ![]() и
подставляются в формулу:
и
подставляются в формулу: ![]() ,
, ![]() ,
, ![]() - всё
это
- всё
это ![]() . Сначала рассмотрим
. Сначала рассмотрим 
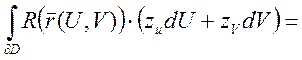
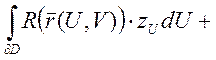
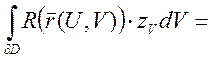 (по формуле Грина)
(по формуле Грина) 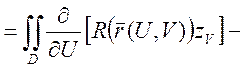
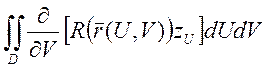
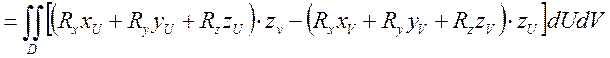
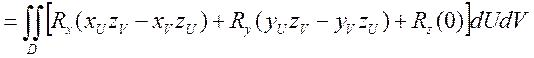
В итоге это всё 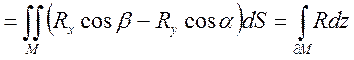
Аналогично для 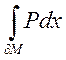 и
и 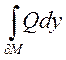 :
: 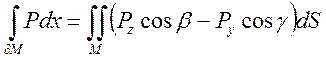 ,
, 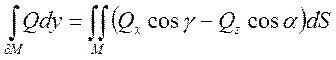 .
Складываем все три интеграла – формула Стокса.
.
Складываем все три интеграла – формула Стокса.
Формула Лейбница
Теорема:
Пусть ![]() и
и
![]() - непрерывно диф. на
- непрерывно диф. на ![]() (
(![]() ), а функция
), а функция ![]() - непрерывно диф-ма по
- непрерывно диф-ма по ![]() ,
, ![]() ,
, ![]()
Тогда имеет место формула
Лейбница: 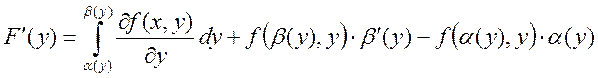
Доказательство: рассмотрим функцию 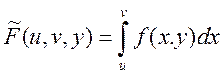 ,
, ![]() - переменные. Заметим, что
- переменные. Заметим, что ![]() - непрерывно диф-ма по обеим переменным.
Поэтому
- непрерывно диф-ма по обеим переменным.
Поэтому 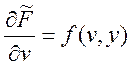 ,
,  ,
, 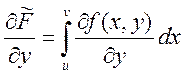 . Если вместо
. Если вместо ![]() , а
вместо
, а
вместо ![]()
![]() .
. 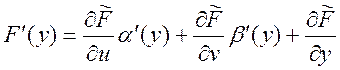 . Если теперь подставим, то получим формулу
Лейбница.
. Если теперь подставим, то получим формулу
Лейбница.
Формула Тейлора
Функция многих переменных в окрестности
точки ![]() представляется в виде некого полинома +
некий остаток.
представляется в виде некого полинома +
некий остаток. ![]() - полином первой степени – однор.
- полином первой степени – однор.
 - однородный полином второй степени. Обычно
симметричная матрица
- однородный полином второй степени. Обычно
симметричная матрица ![]() . В общем случае:
. В общем случае: 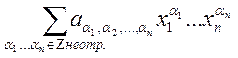 - формульный полином
- формульный полином ![]() -степени.
-степени.
![]()
 +…+
+…+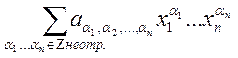
![]() - это формула Тейлора.
- это формула Тейлора.
Но ![]() можно
вычислить, это частные производные:
можно
вычислить, это частные производные: 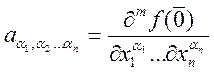 в точке
в точке ![]() .
.
Теорема: пусть функция ![]() имеет
непрерывные частные производные в окрестности точки
имеет
непрерывные частные производные в окрестности точки ![]() порядка
порядка
![]() . Тогда в этой окрестности имеет место
формула Тейлора:
. Тогда в этой окрестности имеет место
формула Тейлора:
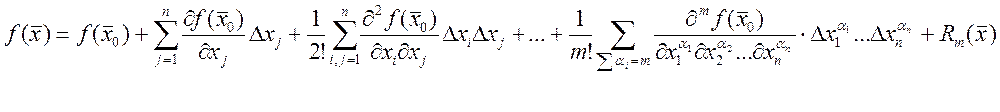
где  -
Формула Лагранжа,
-
Формула Лагранжа, ![]() ,
, ![]() , а
, а ![]()
Доказательство:
Рассмотрим функцию ![]() . Фиксируем
. Фиксируем ![]() и
и ![]() , и пусть
, и пусть ![]() .
Предположим, что
.
Предположим, что ![]() мало, чтобы
мало, чтобы ![]() лежала в окрестности, где функция имеет
непрерывные частные производные. В окрестности точки
лежала в окрестности, где функция имеет
непрерывные частные производные. В окрестности точки ![]() имеет
непрерывные производные
имеет
непрерывные производные ![]()
![]() F
разлагается в ряд Тейлора:
F
разлагается в ряд Тейлора: 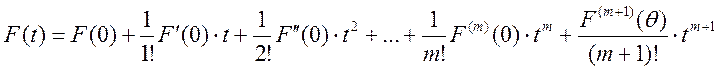 . Полагая в этой
формуле
. Полагая в этой
формуле ![]() и подставляя значение
и подставляя значение ![]() получаем нужную нам формулу Тейлора с
остатком в формуле Лагранжа.
получаем нужную нам формулу Тейлора с
остатком в формуле Лагранжа.
Замечание:

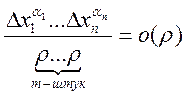
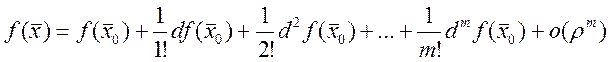
![]() ,
,
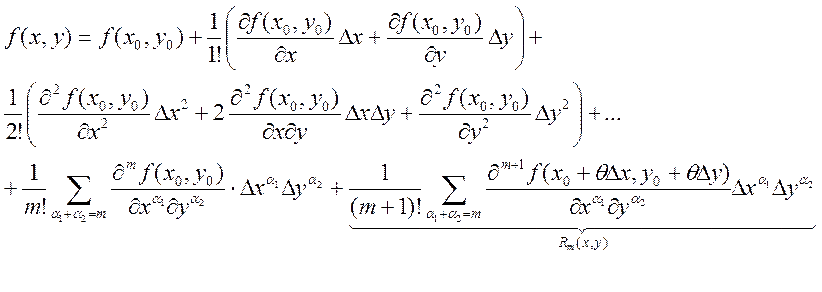
![]() ,
, ![]() ,
,
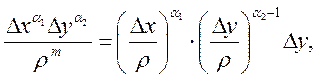
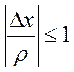 и
и 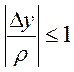
Теперь ![]() ,
, ![]()

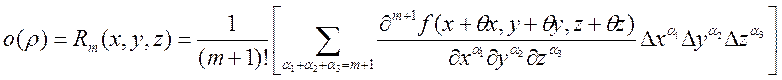
Например: ![]() - разложить в
- разложить в ![]() ,
, 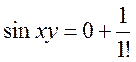 .
. ![]() ,
, ![]() в точке (0,0) это нули. Вторые не
смешанные производные тоже в (0,0) нули, и т.д….
в точке (0,0) это нули. Вторые не
смешанные производные тоже в (0,0) нули, и т.д…. ![]()
Частные производные.
Будем рассматривать только
функции (не вектор-функции) ![]() ,
, ![]() ,
,
Возьмем внутреннюю точку ![]() . Рассмотрим
. Рассмотрим ![]() , (
, (![]() ,
,![]() ),
),![]() и
и ![]() -
числа.
-
числа. ![]() =
=![]() - смещение.
- смещение.
Рассмотрим 1. 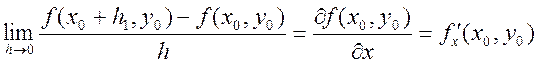 . 2.
. 2. 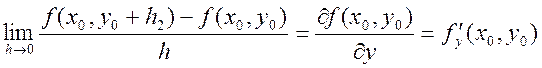 . Если
существуют пределы 1 и 2, то они называются частными производными числами
функции
. Если
существуют пределы 1 и 2, то они называются частными производными числами
функции ![]() в точке
в точке ![]() . Если
функция имеет частные производные в любой точке множества E, то
она имеет частную производную на множестве Е.
. Если
функция имеет частные производные в любой точке множества E, то
она имеет частную производную на множестве Е.
Частные производные высших порядков.
Ех: ![]() ,
,
![]() и
и ![]() ,
, ![]() и
и ![]() .
. ![]() ,
, ![]() ,
, ![]() (
( ![]() , т.к
сначала по x( справа), а потом по y).
, т.к
сначала по x( справа), а потом по y). ![]() ,
, ![]() . Это
индуктивный порядок. Первых производных – n, вторых – n2, третьих – n3,…Частные производные высших порядков определяются
индуктивно. Частные производные были определены ранее – это функции. Мы можем
говорить о частных производных этих функций – частные производные второго
порядка и т.д.
. Это
индуктивный порядок. Первых производных – n, вторых – n2, третьих – n3,…Частные производные высших порядков определяются
индуктивно. Частные производные были определены ранее – это функции. Мы можем
говорить о частных производных этих функций – частные производные второго
порядка и т.д. 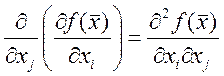 . В некоторых случаях смешанные
производные высших порядков оказываются равными ( если функция непрерывна).
. В некоторых случаях смешанные
производные высших порядков оказываются равными ( если функция непрерывна).
Теорема: пусть функция ![]() ,
, ![]() - непрерывна в D и имеет
непрерывные частные производные второго порядка
- непрерывна в D и имеет
непрерывные частные производные второго порядка 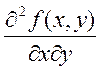 и
и 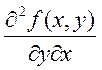 . Тогда
. Тогда 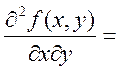
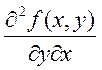
Доказательство: Рассмотрим выражение 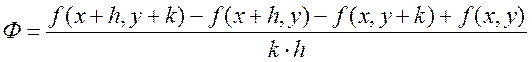 ,
, ![]() ,
, ![]() ,
, ![]() - это числа,
- это числа, ![]() .
.
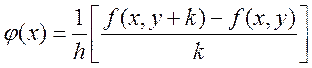 .
.
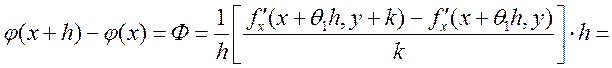
![]()
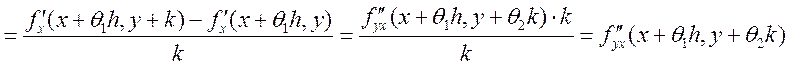
Теперь рассмотрим 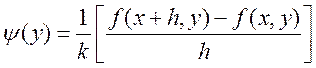 ,
, ![]() , Т.к.
функция непрерывна, то устремляя
, Т.к.
функция непрерывна, то устремляя ![]() и
и ![]()
![]()
![]() .
Ч.т.д.
.
Ч.т.д.
Пример, когда это не верно:
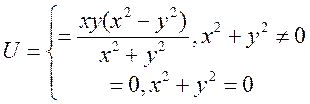 ,
одна производная равна 1, а другая (-1).
,
одна производная равна 1, а другая (-1).
Следствие: пусть функция ![]() имеет в
области D непрерывные производные (частные) m –
ого порядка (m>1). Тогда любую производную m –
ого порядка можно записать в виде:
имеет в
области D непрерывные производные (частные) m –
ого порядка (m>1). Тогда любую производную m –
ого порядка можно записать в виде: 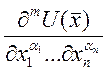 , где
, где ![]() и
и ![]()
Докажем это следствие для
двух переменных: 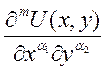 , где
, где ![]() и
и ![]() . По мат. индукции (для двух она доказана)
. По мат. индукции (для двух она доказана) 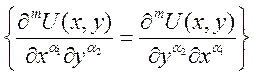 , т.к для m=2 – верно.
Пусть для m – верно. Для m+1 надо
доказать:
, т.к для m=2 – верно.
Пусть для m – верно. Для m+1 надо
доказать: 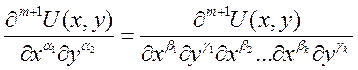 , причем
, причем ![]() ,
, ![]() ,
, ![]()
Элементы векторного анализа (div, grad, rot).
1) ![]() ,
,
![]()
![]()
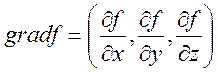 -
градиент. Он всегда ортогонален к множеству уровня (макс. изменение функции
происходит в направление градиента)
-
градиент. Он всегда ортогонален к множеству уровня (макс. изменение функции
происходит в направление градиента)
2) ![]()
![]()
 - дивергенция.
- дивергенция.
3)  -
лапласлан (оператор Лапласа)
-
лапласлан (оператор Лапласа)
![]() -
лапласлан от вектора.
-
лапласлан от вектора.
4) 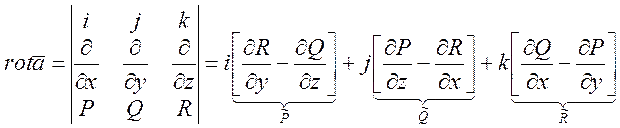 -
вихрь, ротор
-
вихрь, ротор
Утверждение 1
Имеют место равенства: ![]()
1. ![]()
2. ![]()
3. ![]()
4. ![]()
Доказательство:
1. ![]()
2. ![]()
3. тоже подстановкой….
4. 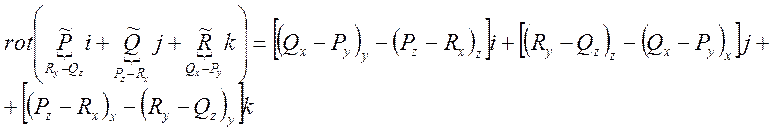
Правая часть: ![]() ,
, ![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.