Докажем это (геометр.):{факт:
если непрерывная функция в некоторой точке > 0![]() окрестность где функция > 0}. Пусть выполнены
условия теоремы, для опр-сти
окрестность где функция > 0}. Пусть выполнены
условия теоремы, для опр-сти 
![]() существует окрестность, где
существует окрестность, где  ,
где
,
где![]() окрестности
окрестности ![]() {квадрат,
пусть сторона
{квадрат,
пусть сторона ![]() }.
}. ![]() фиксируем,
а
фиксируем,
а ![]() меняем по прямой параллельной оси, т.к.
меняем по прямой параллельной оси, т.к. 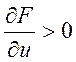 , т.е. функция растёт
, т.е. функция растёт![]() существует окрестность где
существует окрестность где ![]() (сверху).
Поэтому выбираем наименьший интервал, чтобы выпол.
(сверху).
Поэтому выбираем наименьший интервал, чтобы выпол. ![]() (сверху),
(сверху),
![]() (снизу).А вот теперь рассмотрим функцию, не
проходящую через
(снизу).А вот теперь рассмотрим функцию, не
проходящую через ![]() т.к на концах F
принимает разные знаки и непрерывна
т.к на концах F
принимает разные знаки и непрерывна ![]() существует
точка такая, что
существует
точка такая, что ![]() поэтому существует
поэтому существует ![]()
б) m=1, n – любое число.
Справедливо для любой диф.
функции 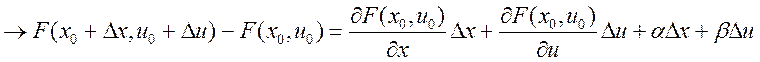 , где
, где ![]() ,
, ![]() , т.е
, т.е 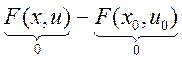 - при
- при
![]() , тогда
, тогда ![]() . Тогда
. Тогда
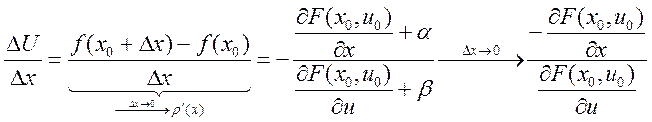 , т.е.
, т.е. 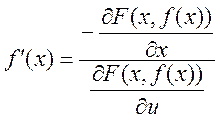 ,
т.к.
,
т.к. ![]() - непрерывна,
- непрерывна, ![]() ,
заменим
,
заменим ![]() частн. произв.
частн. произв. ![]() -
непрерывна.
-
непрерывна.
2) m=1, n –
любое ![]()

![]() частная производная непрерывна.
частная производная непрерывна.
3) общий случай: m и n –
любые числа (целые). По методу мат. индукции: (по числу m) .
Пусть справедливо для ![]() . Запишем матрицу Якоби:
. Запишем матрицу Якоби:  в точке
в точке ![]() .
Якобиан в точке
.
Якобиан в точке ![]() - определитель. Рассмотри
последнюю строку: по крайне мере одно число
- определитель. Рассмотри
последнюю строку: по крайне мере одно число ![]() . Пусть
последнее число
. Пусть
последнее число  . Тогда рассмотрим
. Тогда рассмотрим ![]() :
: ![]() , а
, а ![]() .
. ![]() по
свойству.
по
свойству. ![]() - частная производная по
- частная производная по ![]() отлична от 0. Тогда эта функция
удовлетворяет условия теоремы m=1 и n=m-1+n. Тогда существует неявная функция
отлична от 0. Тогда эта функция
удовлетворяет условия теоремы m=1 и n=m-1+n. Тогда существует неявная функция ![]() ,
, ![]() ,
, ![]() - имеет непрерывные частные производные.
Посчитаем их:
- имеет непрерывные частные производные.
Посчитаем их: 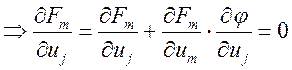 , т.к. производная от 0 равна0.
Строим функции
, т.к. производная от 0 равна0.
Строим функции ![]() , которые зависят от
, которые зависят от ![]() . В итоге :
. В итоге : ![]()
![]() . Теперь нужно проверить условие о неявной
функции. Всё кроме того, что якобиан не равен нулю, понятно!
. Теперь нужно проверить условие о неявной
функции. Всё кроме того, что якобиан не равен нулю, понятно!
Докажем что якобиан для Ф ![]() . Запишем его:
. Запишем его: 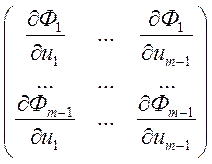 в
точке
в
точке ![]() - надо доказать
- надо доказать
Докажем, что якобиан не равен
0: 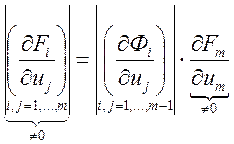 , то
, то  .
Подставим в
.
Подставим в ![]()
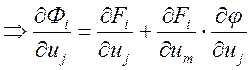 - диф-ние сложных
функций (
- диф-ние сложных
функций (![]() ).Т.к.
).Т.к. ![]() продиф-ем
продиф-ем
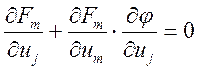 , где
, где ![]()
Определитель матрицы не
меняется, если столбцы матрицы умножить на число и прибавить к другому столбцу.
Посл. Столбец 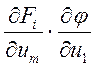 и прибавим к первому
и прибавим к первому ![]() получим первый столбец матрицы Ф. Со
вторым - та же операция. Но, когда к первому столбцу приб. последний (умножен.
на
получим первый столбец матрицы Ф. Со
вторым - та же операция. Но, когда к первому столбцу приб. последний (умножен.
на ![]() ), то первый столбец
), то первый столбец ![]() для элементов до (m-1) , т.к.
совпадает с , а последний элемент =0,т.к.
для элементов до (m-1) , т.к.
совпадает с , а последний элемент =0,т.к. 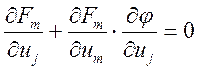 .
Тогда разлагается по последней строке
.
Тогда разлагается по последней строке![]()
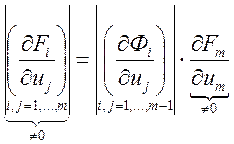 . Подставим , получим неявную функцию в
окрестности.
. Подставим , получим неявную функцию в
окрестности.
Теорема о равенстве двойного интеграла повторному
Теорема:
Если ![]() -
непрерывна на Е и функции
-
непрерывна на Е и функции ![]() - непрерывна на
- непрерывна на ![]() . Тогда существует
. Тогда существует 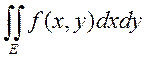 -
двойной интеграл по Е, и существует повторный интеграл
-
двойной интеграл по Е, и существует повторный интеграл 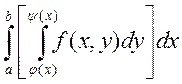 и
они равны, т.е
и
они равны, т.е 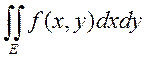
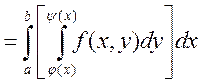
Доказательство: то, что
двойной интеграл существует, доказано (Е=К – компакт измеримый) ![]() существует
существует  . Надо
доказать, что существует повторный интеграл, и он равен двойному.
. Надо
доказать, что существует повторный интеграл, и он равен двойному.
Существование: ![]() - непрерывна, если
фиксируем х
- непрерывна, если
фиксируем х ![]() - компакт
- компакт ![]() существует
существует
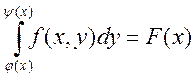 - всякая непрерывная ограниченная функция.
Покажем, что
- всякая непрерывная ограниченная функция.
Покажем, что ![]() - интегрируема по Риманау. Для этого
покажем, что она непрерывна, т.к. любая непрерывная функция интегрируема по
Риману. Замена переменных:
- интегрируема по Риманау. Для этого
покажем, что она непрерывна, т.к. любая непрерывная функция интегрируема по
Риману. Замена переменных: ![]() ,
, ![]() меняется от 1 до 0.
меняется от 1 до 0. ![]()
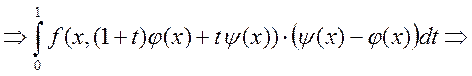
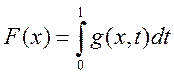 -
получили. g – это непрерывная функция двух переменных, т.к.
-
получили. g – это непрерывная функция двух переменных, т.к. ![]() , а
, а ![]() .
.
Рассмотрим разность: 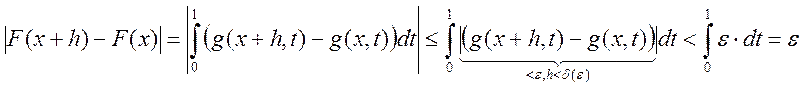 , ||g – непрерывна,
наш прямоугольник – компакт,
, ||g – непрерывна,
наш прямоугольник – компакт, ![]() по теореме Кантора –
равномерно непрерывна|| т.е
по теореме Кантора –
равномерно непрерывна|| т.е ![]() , т.е функция
непрерывна при
, т.е функция
непрерывна при ![]() . Всё, F(x) –
непрерывна
. Всё, F(x) –
непрерывна ![]() интегрируема по Риману
интегрируема по Риману ![]() повторный интеграл существует.
повторный интеграл существует.
Равенство интегралов: рассмотрим  ,
, ![]() - это всё непрерывные функции.
- это всё непрерывные функции. ![]() -
- ![]() ,
, ![]() - выше (
- выше (![]() ), …
), …
![]() разбиваем
на k частей (
разбиваем
на k частей (![]() ). Проведём прямые
параллельно OY через точки
). Проведём прямые
параллельно OY через точки ![]() получаем
разбиение
получаем
разбиение ![]()
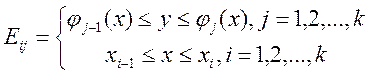 , Это разбиение
, Это разбиение ![]() измеримо по Жордану,
измеримо по Жордану, ![]() .
.  -
площадь кусочка. Вводим
-
площадь кусочка. Вводим 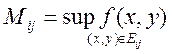 ,
,  . Рассмотрим повторный интеграл:
. Рассмотрим повторный интеграл: 

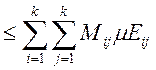 {т.к.
{т.к.
![]() для
для ![]() }
} ![]()

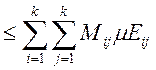 .
(
.
(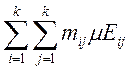 ,
, - суммы Дарбу для
двойного интеграла). Т.к.
- суммы Дарбу для
двойного интеграла). Т.к. ![]() интегрируема по Риману,
то
интегрируема по Риману,
то 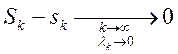 ,
, ![]() и
и ![]()
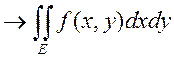 . Ч.т.д.
. Ч.т.д.
Если несколько переменных ![]() аналогично:
аналогично: 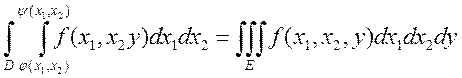 и
т.д.
и
т.д. ![]() ,
, ![]() -
строго выпуклое множество. Тогда существует
-
строго выпуклое множество. Тогда существует 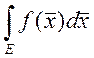 .
.
Теорема Римана
Пусть ![]() ,
- непрерывная функция, тогда
,
- непрерывная функция, тогда 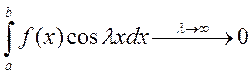 и
и  {интеграл – сумма всех площадей. Они друг
друга «гасят» - в пределе – 0.}
{интеграл – сумма всех площадей. Они друг
друга «гасят» - в пределе – 0.}
Доказательство: Рассмотрим 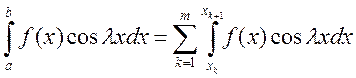

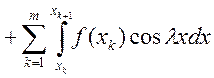
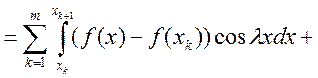
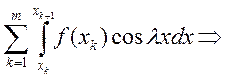
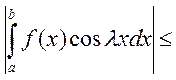
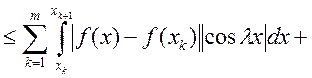
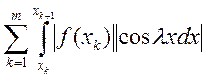 . По теореме Кантора
. По теореме Кантора ![]() ,
, ![]() . Пусть
максимальное разбиение =
. Пусть
максимальное разбиение = ![]() и
и ![]() . Тогда
. Тогда ![]() . Тогда
. Тогда
 ,
, 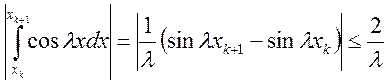 .
Тогда
.
Тогда 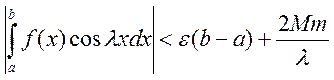 . Т.е
. Т.е 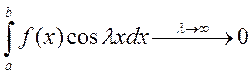 , т.к
, т.к ![]() меняется независимо от m.
меняется независимо от m.
Теорема: пусть ![]() - непрерывная функция.
И выполнены условия: 1) функция
- непрерывная функция.
И выполнены условия: 1) функция ![]() имеет обратную
имеет обратную ![]() . Обратная – единственная. 2) метрическое
пространство
. Обратная – единственная. 2) метрическое
пространство ![]() является компактом. Тогда обратная функция
является компактом. Тогда обратная функция
![]() непрерывна на
непрерывна на ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.