Доказательство: ![]() - надо доказать, что непрерывна
- надо доказать, что непрерывна ![]() 1)
1) ![]() и
и ![]()
![]() ; 2) Надо док-ть
противное,
; 2) Надо док-ть
противное, ![]()
![]() -
отрицание ; 3) пусть
-
отрицание ; 3) пусть 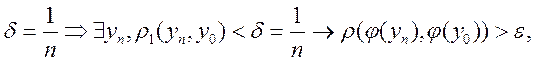
![]() ; 4)
; 4) 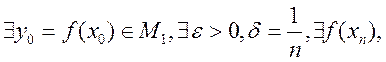 что
что 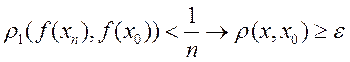 -
неравенство*. Выделим сход. подпослед.
-
неравенство*. Выделим сход. подпослед. ![]() т.к.
т.к. ![]() . Докажем, что
. Докажем, что ![]()
![]() по непрерывности
по непрерывности ![]() подставим
в неравенство*:
подставим
в неравенство*: 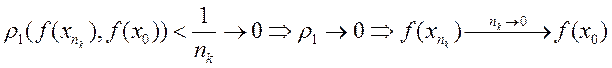 .В силу единственности предела
.В силу единственности предела ![]() , а т.к. существует обратная единственная
функция
, а т.к. существует обратная единственная
функция ![]() . Тогда
. Тогда ![]() - мы
доказали. Но из неравенства*
- мы
доказали. Но из неравенства* ![]() - то эти 2 соотнош.
против.
- то эти 2 соотнош.
против.
Теорема Эйлера об однородной функции
Для того чтобы диф-мая
функция ![]() ,
, ![]() , была
положительно однородной степени
, была
положительно однородной степени ![]() необходимо и
достаточно, что бы выполнялось равенство :
необходимо и
достаточно, что бы выполнялось равенство : 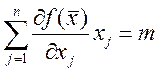
![]() ,
, ![]()
Доказательство:
1) пусть функция однородна ![]() докажем, что выполняется
докажем, что выполняется 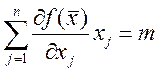
![]() ,
, ![]() . Пусть
. Пусть ![]() -
однородна, т.е.
-
однородна, т.е. ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Фиксируем
. Фиксируем
![]() и рассмотрим
и рассмотрим ![]() -
меняющееся. Диф-ем обе части
-
меняющееся. Диф-ем обе части ![]()
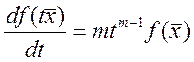 .
.
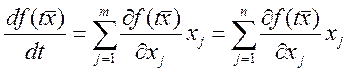 , т.к.
, т.к. ![]() .
Полагаем, что
.
Полагаем, что ![]()
![]()
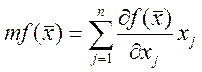 . Для любой точки
. Для любой точки ![]() это
выполнено.
это
выполнено.
2) пусть выполнено равенство 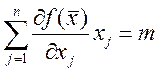
![]() ,
, ![]() . Докажем, что
. Докажем, что ![]() -
однородность. Фиксируем
-
однородность. Фиксируем ![]() и рассмотрим функцию
и рассмотрим функцию![]() :
:
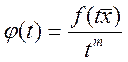 ,
, ![]() .
. ![]() -
диф-ма, знаменатель
-
диф-ма, знаменатель ![]() .
. 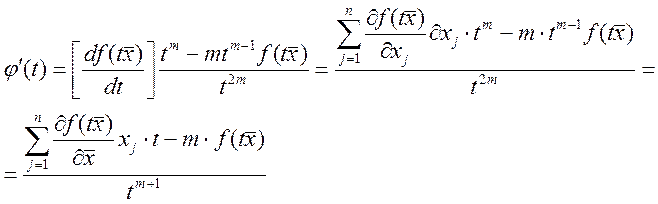
Числитель = 0, т.к. это
соотношение 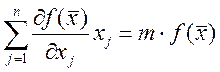 , только в точке
, только в точке ![]() . Поэтому
. Поэтому ![]() , значит
, значит
![]() . Полагая, что
. Полагая, что ![]() , видим,
что
, видим,
что ![]()
![]()
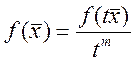
![]()
![]() , при
, при ![]() ,
, ![]() .
.
Теория локального экстремума для функции многих переменных
Если производная чётная(чётного порядка), то экстремуму нет.
Необходимые условия экстремуму – частные производные = 0
Достаточные условия экстремума – три частные производные второго порядка, рассмотрим второй диф-ал: если квадратичная ф-ма положит. определ., то экстремум будет min, а если отриц. то max
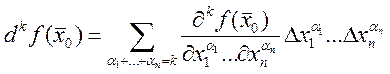 -
диф-ал
-
диф-ал ![]() -того порядка.
-того порядка.
Опр.: функция ![]() ,
, ![]() , D – область, имеющая во
внутренней точке
, D – область, имеющая во
внутренней точке ![]() экстремум, если существует
окрестность
экстремум, если существует
окрестность ![]() , такая что
, такая что ![]() выполнено
одно из двух неравенств:
выполнено
одно из двух неравенств: ![]() , либо
, либо ![]() . При этом, если
. При этом, если ![]() ,
,
![]() , то точка
, то точка ![]() - строго
min, либо
- строго
min, либо ![]() ,
, ![]() , то точка
, то точка ![]() - строго
max.
- строго
max.
Теорема (необходимые условия экстремума) :
если в точке ![]() , D – область имеющая экстремум, и
в этой точке
, D – область имеющая экстремум, и
в этой точке 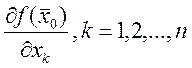 , то
, то 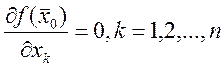
Доказательство: т.к. экстремум ![]() существует
окрестность из D, что выполнено одно из неравенств:
существует
окрестность из D, что выполнено одно из неравенств: ![]() , либо
, либо ![]() ,
, ![]() . Фиксируем все переменные кроме k-ой
. Фиксируем все переменные кроме k-ой ![]() рассмотрим
рассмотрим ![]() -
чтобы точка не выходила из окрестности. Эта функция от одной переменной
-
чтобы точка не выходила из окрестности. Эта функция от одной переменной ![]() в
в ![]()
![]() достигает экстремума, эта точка внутренняя
достигает экстремума, эта точка внутренняя
![]() max или min
max или min ![]() существует производная
существует производная![]() по теореме Ферма
по теореме Ферма 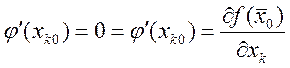 .
Ч.т.д.
.
Ч.т.д.
Т.е. если функция в какой-то точке дост. локального max или min, и существует частн. производные, то все они равны нулю.
Теорема (достаточные условия):
Пусть функция ![]() дважды непрерывно диф-ма в области
дважды непрерывно диф-ма в области ![]() и существует точка
и существует точка ![]() ,
такая что
,
такая что
1) 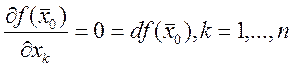
2) ![]() либо
либо
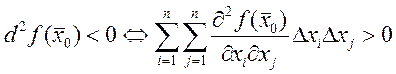 либо
либо 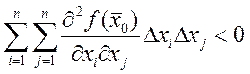 , при
, при ![]() . Тогда в точке
. Тогда в точке ![]() -
экстремум:
-
экстремум:
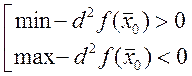
Доказательство:
т.к. она дважды непрерывно
диф-ма ![]() разлагается в строку Тейлора:
разлагается в строку Тейлора: 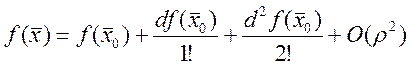 , где
, где ![]() .
. 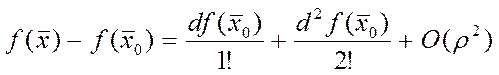 - это квадратичная форма относ.
- это квадратичная форма относ. ![]() выберем окрестность, чтобы знак квадр.
формы совпадал со знаком любой части.
выберем окрестность, чтобы знак квадр.
формы совпадал со знаком любой части.
1) пусть ф-ма >0 ![]()
![]() , т.е.
, т.е. ![]()
2) пусть ф-ма >0 ![]()
![]() , т.е.
, т.е. ![]()
Теорема: пусть ![]() дважды непрерывно
диф-ма в
дважды непрерывно
диф-ма в ![]() и выполнены условия
и выполнены условия
1) ![]()
2) ![]() .
Тогда в точке
.
Тогда в точке ![]() - экстремум max,
если
- экстремум max,
если ![]() , или min, если
, или min, если ![]()
3) если же ![]() , то экстремума в точке
, то экстремума в точке ![]() - нет.
- нет.
4) и если ![]() , то неопределенность в точке
, то неопределенность в точке ![]() - экстремум может быть, а может и нет.
- экстремум может быть, а может и нет.
Доказательство:
1) пусть ![]() и
и ![]() .
Докажем, что квадратичная форма
.
Докажем, что квадратичная форма ![]() либо >0, либо <0
либо >0, либо <0
![]() существует экстремум в точке
существует экстремум в точке ![]()
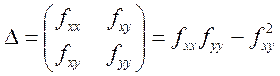 - определитель. Пусть
- определитель. Пусть ![]() . Т.к.
. Т.к. ![]()
![]() квадр. форма равна =
квадр. форма равна = 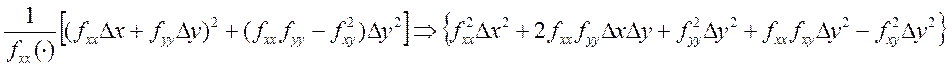
![]() квадратная
скобка
квадратная
скобка ![]() знак выражения зависит от знака
знак выражения зависит от знака ![]() , если
, если ![]() выражение
> 0 , а если
выражение
> 0 , а если ![]() выражение < 0
выражение < 0
2) пусть ![]() . Тогда возможны случаи:
. Тогда возможны случаи:
* пусть ![]() см. на
см. на 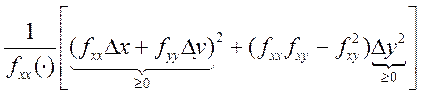 .
Покажем что квадр. форма имеет знак . Пусть
.
Покажем что квадр. форма имеет знак . Пусть ![]() . Пусть
. Пусть
![]()
* а если ![]() (либо
(либо ![]() )
)![]() рассужд. повтор.
рассужд. повтор.
* а если ![]() форма тоже имеет знак при изменение знака
форма тоже имеет знак при изменение знака ![]() и
и ![]() .
Поэтому экстремума нет.
.
Поэтому экстремума нет.
3) пусть ![]() . Будем приводить примеры. 1. пусть
. Будем приводить примеры. 1. пусть ![]() - экстремум есть в (0,0). И
- экстремум есть в (0,0). И ![]() этой функции
этой функции ![]() .2.
.2. ![]() - меняет знак
- меняет знак ![]() нет
экстремума,
нет
экстремума, ![]()
Достаточные условия экстремума в общем случае:
Теорема: пусть функция ![]() ,
, ![]() раз непрерывно диф-ма в области
раз непрерывно диф-ма в области ![]() . И существует точка
. И существует точка ![]() , такая что
, такая что
1) ![]() ,
,
2) ![]() тогда
если m – нечетное число, то экстремума в
тогда
если m – нечетное число, то экстремума в ![]() нет. А если m – четное число
и плюс к этому
нет. А если m – четное число
и плюс к этому ![]() либо
либо ![]() , то в
точке
, то в
точке ![]() экстремум {max, если
экстремум {max, если ![]() , min если
, min если ![]() }
}
Доказательство:
т.к ![]() имеет
непрер. частные производные m-ого порядка → Тейлор:
имеет
непрер. частные производные m-ого порядка → Тейлор:
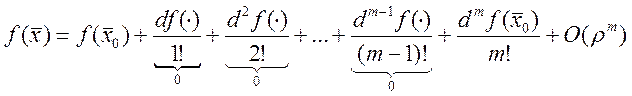 ,
, ![]() , а
, а 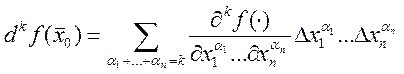 , где
, где ![]() ,
, 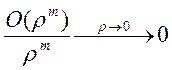 ,
, ![]() . Поэтому
. Поэтому 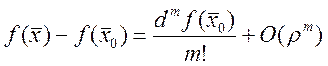 . Знак
разности
. Знак
разности ![]() опред. только знаком, т.к
опред. только знаком, т.к ![]() очень мало. При нечетной степени m –
меняет знак, т.е. экстремума нет {нечетная функция степени m
меняет знак в окрестности
очень мало. При нечетной степени m –
меняет знак, т.е. экстремума нет {нечетная функция степени m
меняет знак в окрестности ![]() }. А если m
четное число, то надо рассмотреть ф-му. Если
}. А если m
четное число, то надо рассмотреть ф-му. Если ![]() в
некоторой окрестности и
в
некоторой окрестности и ![]() тоже
тоже ![]() - точка max. А если
- точка max. А если ![]() ,
, ![]()
![]() - точка min.
- точка min.
Формула Грина
Теорема:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.