







Решение задач на контрольной 9 апреля 2000 г.
Группа 646-741-742
 1. (400) Определить разрешенность по симметрии реакции
диссоциации BH3 ® BH + H2. Построить корреляционную диаграмму и оценить
изменение энергии в этой реакции. BH3 – плоская молекула. Считать кулоновские интегралы
орбиталей атомов B (2s, 2p) и H (1s) одинаковыми. Энергии связи B-H и H-H
тоже одинаковы.
1. (400) Определить разрешенность по симметрии реакции
диссоциации BH3 ® BH + H2. Построить корреляционную диаграмму и оценить
изменение энергии в этой реакции. BH3 – плоская молекула. Считать кулоновские интегралы
орбиталей атомов B (2s, 2p) и H (1s) одинаковыми. Энергии связи B-H и H-H
тоже одинаковы.
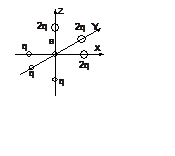
2. (400) Определить расщепление между самой высокой по энергии p-орбиталью и самой низкой для иона с конфигурацией p1 в поле 6 лигандов, 3 из которых имеют заряд q, а три других - заряд 2q (см. рисунок). Расстояния до всех лигандов равны а.
3. (400) Квантовый выход люминесценции красителя родамина 6G в полистироле равен 1. Введение в полимер молекул акцептора в концентрации 10-3 M уменьшает квантовый выход до 10-2. По какому механизму (диполь-дипольному или обменному) происходит тушение люминесценции? Ответ обосновать.
4 (400) Определить степень поляризации люминесценции при облучении кольца из тонкой полимерной нити. В полимере растворены молекулы красителя, дипольный момент которых направлен вдоль нити. Плоскость кольца наклонена под углом a к оси Z. Возбуждающий свет распространяется вдоль оси X и поляризован по Z. Регистрация люминесценции производится вдоль оси X.
5. (400) Определить разрешен ли по симметрии дипольный переход между самой нижней и самой высокой по энергии орбиталями для плоской циклической молекулы Hn (n = 4k+2, где k – целое число). Если разрешен, определить поляризацию перехода.
6. (1000) Определить расщепление d-орбиталей для иона с конфигурацией d1 в поле лигандов, аналогичных в задаче 2.
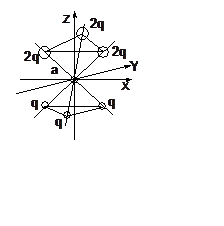
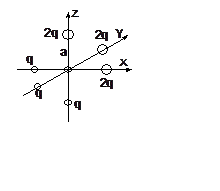 Решение: Повернем оси, как указано на втором рисунке, и
определим, что группа симметрии - С3v, в
которой по полносимметричному представлению преобразуются гармоники Y00, Y20, Y40, (Y43+Y4-3). Они и могут войти в потенциал кристаллического
поля. Для угла между осью Z и направлением на лиганды из простых геометрических
расчетов следует, что
Решение: Повернем оси, как указано на втором рисунке, и
определим, что группа симметрии - С3v, в
которой по полносимметричному представлению преобразуются гармоники Y00, Y20, Y40, (Y43+Y4-3). Они и могут войти в потенциал кристаллического
поля. Для угла между осью Z и направлением на лиганды из простых геометрических
расчетов следует, что 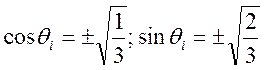 . Из-за того, что
. Из-за того, что ![]() , для вышеприведенных угловых координат
лигандов эта гармоника будет равна нулю и не войдет в оператор кристаллического
поля, который для такого комплекса будет иметь вид
, для вышеприведенных угловых координат
лигандов эта гармоника будет равна нулю и не войдет в оператор кристаллического
поля, который для такого комплекса будет иметь вид
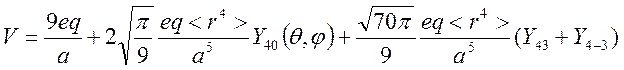
Этот оператор выражается через эквивалентные операторы следующим образом
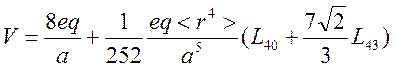
Матричные элементы
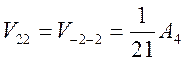
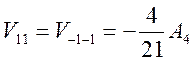
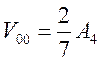
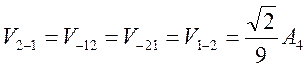
В итоге, искомое расщепление между орбиталями равно
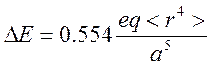
Задачи на контрольную 8 апреля 2001. Группы 841-842-743
1. (600) Как изменится расстояние между dxy и dx2-y2 орбиталями, если в октаэдрическом комплексе d1 иона удалить один из лигандов, расположенных вдоль оси z?
Решение: Для октаэдрического комплекса расстояние между орбиталями dxy и dx2-y2 равно
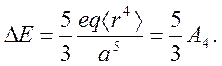
При удалении лиганда вдоль оси z, группа симметрии понизится до C4v. В этой группе в потенциал кристаллического поля войдут гармоники Y00, Y20, Y40, (Y44+Y4-4). После определения угловых координат лигандов и замены гармоник на эквивалентные операторы оператор кристаллического поля приобретает вид (Y00 опускаем)
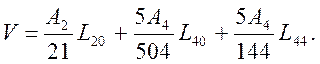
где
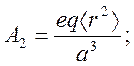
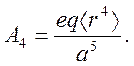
Матричные элементы с оператором кристаллического поля равны
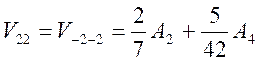 ;
; 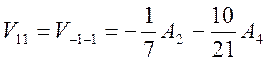 ;
; 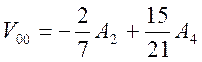 ;
; 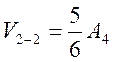
Детерминант для гармоник Y22 и Y2-2 (орбитали dxy и dx2-y2) дает корни
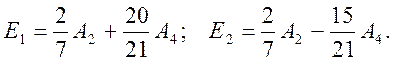
и расщепление между орбиталями dxy и dx2-y2 становится равным разности этих корней
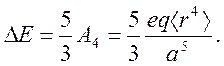
Таким образом, расстояние между орбиталями dxy и dx2-y2 при удалении лиганда не изменяется.
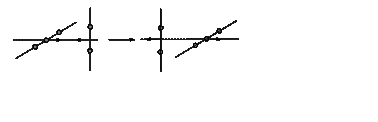
2. (300) Определить разрешенность по симметрии реакции Hn + Hn+1 ® Hn+1 + Hn (геометрия сближения показана на рисунке).
 Решение:
Пусть n будет четным числом, принимающим значения 4k и 4k+2. Введем операцию
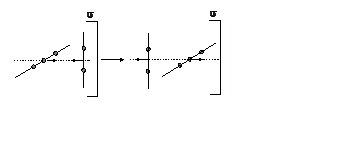
симметрии – плоскость отражения, показанную на рисунке. Подсчитывая число узлов
для орбитали, можно показать, что при n = 4k число симметричных и
антисимметричных орбиталей (включая уровень с энергией ) у начальных и
конечных продуктов совпадают (s – 3k+1, a – k) и реакция разрешена термически.
Для n = 4k+2 у исходных продуктов s – 3k+2, a – k+1. У конечных продуктов s –
3k+3 и a – k. В этом случае реакция запрещена.
Решение:
Пусть n будет четным числом, принимающим значения 4k и 4k+2. Введем операцию
симметрии – плоскость отражения, показанную на рисунке. Подсчитывая число узлов
для орбитали, можно показать, что при n = 4k число симметричных и
антисимметричных орбиталей (включая уровень с энергией ) у начальных и
конечных продуктов совпадают (s – 3k+1, a – k) и реакция разрешена термически.
Для n = 4k+2 у исходных продуктов s – 3k+2, a – k+1. У конечных продуктов s –
3k+3 и a – k. В этом случае реакция запрещена.
3. (300) Для линейной молекулы Hn указать поляризацию перехода S0 ® S1. Считать, что ось молекулы является осью Z. Указать термы, между которыми происходит переход. Считать, что уровни энергии не вырождены.
Решение: Основной терм S0 - 1Sg+ ввиду заполнения двумя электронами невырожденных орбиталей. Так как все орбитали s - типа, возбужденный терм S1 тоже S+ типа. Переход разрешен между орбиталями разной четности, поэтому это будет терм 1Su+. Ввиду того, что DL = 0, переход поляризован вдоль оси Z.
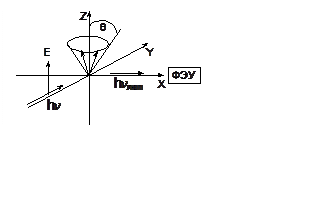 4. (400) Определить степень поляризации при
возбуждении образца поляризованным светом, если дипольные моменты молекул
распределены по поверхности конуса и наклонены к оси Z под углом q. Геометрия эксперимента показана на рисунке. Чему должен быть равен
угол q, чтобы степень поляризации была равна нулю.
4. (400) Определить степень поляризации при
возбуждении образца поляризованным светом, если дипольные моменты молекул
распределены по поверхности конуса и наклонены к оси Z под углом q. Геометрия эксперимента показана на рисунке. Чему должен быть равен
угол q, чтобы степень поляризации была равна нулю.
Решение: Вероятность поглощения пропорциональна cos2q. Вероятность испускания с поляризацией вдоль оси Z тоже
пропорциональна cos2q![]()
Iz = Acos4q.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.