Определение разрешенности по симметрии реакции диссоциации. Определение расщепления между самой высокой по энергии p-орбиталью и самой низкой для иона, страница 2

В плоскости XY проекции дипольных моментов равномерно распределены по кругу, поэтому

.

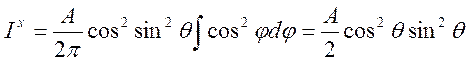Таким образом,

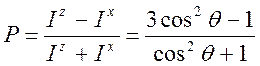. При cos²q = 1/3  P = 0. Угол q = 54.74⁰ – угол Брюстера.

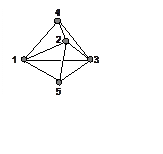
5. (400) Определить основной терм, энергии и поляризацию переходов для радикала H₅, имеющего строение D_3h. На рисунке указаны связи. Все резонансные интегралы считать одинаковыми.

Решение: Можно показать, что в группе D_3h атомные орбитали водородов реализуют НП 2а₁', a₂'' и e'. Комбинации, преобразующиеся по этим представлениям имеют вид

  

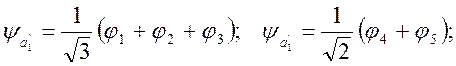
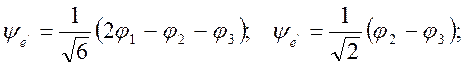
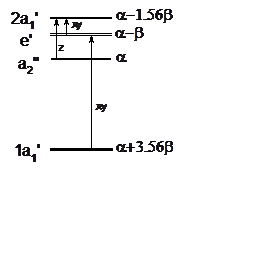
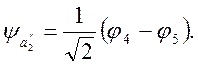 Детерминант для НП а₁' имеет вид 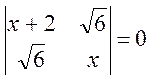, корни которого равны  Энергии орбиталей e' и a₂'' равны a-b и a. На рисунке показано расположение и энергии МО, а также поляризация и положение линий поглощения, которые определяются правилами отбора. Основной терм радикала – ²E'.

Задачи на контрольную 7 апреля 2002. Группы 941-942-943-843

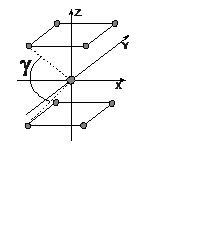
1. (600) Для комплекса MX₈ (ион с 3d¹ электронной конфигурацией, группа симметрии D_4h) найти зависимость расстояния между d_xy и d_x2-y2 орбиталями от угла  (см. рисунок).

Решение:

В группе D_4h в потенциал кристаллического поля войдут гармоники Y₀₀, Y₂₀, Y₄₀, (Y₄₄+Y_4-4). После определения угловых координат лигандов и замены гармоник на эквивалентные операторы оператор кристаллического поля приобретает вид (член V₀₀ = 8eq/a от гармоники Y₀₀ опускаем)

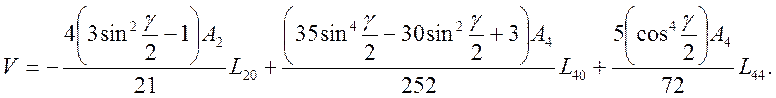
где

   

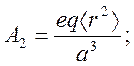
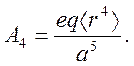
Расстояние между орбиталями d_xy и d_x2-y2 определяется недиагональным матричным элементом между гармоникам Y₂₂ и Y_2-2 , определяемым оператором L₄₄.

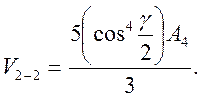
Расщепление между орбиталями d_xy и d_x2-y2 равно 2V_2-2

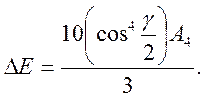
При 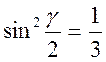 комплекс имеет строение куба, который можно рассматривать как два вложенных друг в друга тетраэдра. В этом случае расстояние между орбиталями d_xy и d_x2-y2

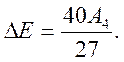
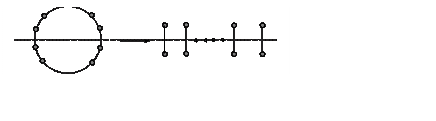
2. (300) Определить разрешенность по симметрии реакции распада плоской циклической молекулы на n молекул водорода (H_2n ® nH₂, см. рисунок).

Решение: Если выбрать в качестве элемента симметрии плоскость, перпендикулярную плоскости исходной циклической молекулы, среди ее связывающих орбиталей будут и антисимметричные. Для конечного состояния молекул водорода антисимметричные орбитали будут только среди разрыхляющих. Таким образом, реакция запрещена для реализации термическим способом.

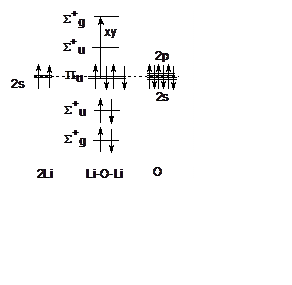
3. (400) Для линейной молекулы Li-O-Li указать поляризацию и энергию перехода S₀ ® S₁. Считать, что ось молекулы является осью Z. Кулоновские интегралы орбиталей 2s, 2p кислорода и 2s лития считать одинаковыми. Резонансный интеграл 2s_Li-2s_O в два раза больше резонансного интеграла 2s_Li-2p_O. Указать термы, между которыми происходит переход.

Решение: На рисунке изображены орбитали молекулы и приведена их симметрия. Основной терм S₀ - ¹S_g⁺ ввиду заполнения электронами орбиталей. Возбужденный, нижний по энергии, терм S₁ ¹_u типа. Так как в группе D_¥h компоненты дипольного момента d_x и d_y преобразуются также по _u представлению, переход поляризован вдоль осей XY. Энергия перехода равна DE = b_2sLi-2sO.

4. (300) Шарообразные молекулы радиусом 10 А плотноупакованным мономолекулярным слоем находятся на поверхности кварцевой пластинки. Молекулы имеют полосу поглощения с коэффициентом экстинкции в ее максимуме e = 6´10⁵ л/моль´см. Определить оптическую плотность такой пластинки в на длине волны максимума полосы поглощения. Считать, что кварц не поглощает и не отражает свет.

Решение: Сечение поглощения молекулой равно s = e/N₀ = 10^-15 см². Площадь, занимаемая молекулой на пластинке, равна S = (2R)² = 4´10^-14 см². Доля поглощенного света

I_погл/I₀ = (1 – 10^-D) = (1 - exp(-2.3´D)) = s/S = 1/40.

Оптическая плотность будет небольшой (D << 1), поэтому экспоненту можно разложить в ряд и получить

D = 1/(2.3´40) = 0.0108

5. (400) Определить энергии и поляризацию переходов для комплекса TiH₄³⁺ (ион Ti³⁺ - 3d¹ электронная конфигурация), имеющего строение D_4h. Резонансные интегралы 3d_z2 – 1s и 3d_xz – 1s считать в два раза меньше резонансных интегралов 3d_xy – 1s и 3d_x2-y2 – 1s (если понадобятся какие-то из этих интегралов). Кулоновские интегралы для 3d орбиталей иона титана и 1s атомов водорода считать одинаковыми.

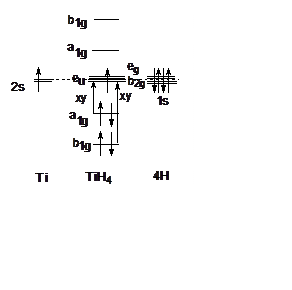Решение: Можно показать, что в группе D_4h 3d орбитали титана преобразуются по представлениям а_1g, b_1g, b_2g и e_g, а атомные орбитали водородов реализуют НП а_1g, b_1g и e_u. Комбинации орбиталей водорода, преобразующиеся по этим представлениям имеют вид

  

  

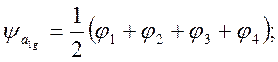
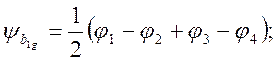
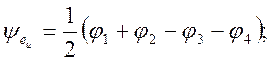
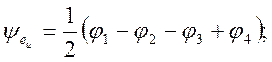
МО а_1g (3d_z2) равны a ± b(3d_z2 – 1s), МО b_1g (3d_x2-y2) равны a ± b(3d_x2-y2 – 1s). Остальные орбитали остаются несвязывающими. На рисунке показано расположение МО, а также положение переходов для двух линий поглощения с XY поляризация, отличающихся по энергии в два раза.

Решение задач на контрольную 6 апреля 2003 г. Группы 041-043

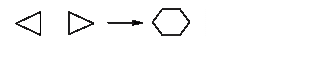1. (400) Определить разрешенность реакции H₃ + H₃®H₆. Построить коррелляционную диаграмму для этой реакции и определить изменение полной электронной энергии. Кулоновские интегралы одинаковы для обоих типов молекул.