Определение разрешенности по симметрии реакции диссоциации. Определение расщепления между самой высокой по энергии p-орбиталью и самой низкой для иона, страница 3

Решение: Начальные и конечная молекулы являются циклическими p-системами, для которой уровни энергии и молекулярные орбитали хорошо известны, поэтому построить корреляционную диаграмму достаточно просто. Изменение полной энергии равно 2b, реакция разрешена.

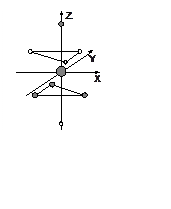
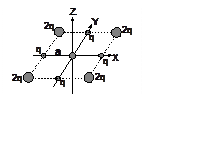
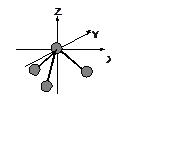
2. (400) Определить расщепление d-орбиталей иона с конфигурацией d¹ в поле 8 лигандов. Темные имеют заряд -q, светлые – -2q. Треугольники правильные, развернуты относительно друг друга на 180⁰ с центрами на оси Z. Ион расположен посередине между треугольниками. Расстояние между центрами треугольников в 3 раза меньше расстояния между лигандами на оси Z. Отношение расстояния от иона до лиганда на оси Z к расстоянию от лигандов, находящихся в углах треугольников, до оси Z равно .

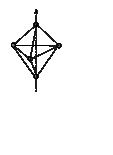Решение: Можно проверить, что при данном соотношении расстояний данная конфигурация расположения лигандов отвечает кубу, составленному из двух вложенных тетраэдров с зарядами –q и –2q. Расщепление d-орбиталей в поле тетраэдра хорошо известно и в этом случае равно (60/27)(eq<r⁴>/a⁵).

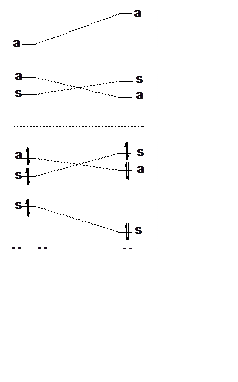
3. (500) Для молекулы H₅, строение которой показано на рисунке (группа D_3h), определить энергию и поляризацию полосы поглощения, отвечающей самому длинноволновому, разрешенному по симметрии переходу. Связи между атомами показаны сплошными линиями. Все резонансные интегралы считать одинаковыми.

Решение: Энергия длинноволнового перехода равна 0.65b. Молекулярные орбитали и симметрия уровней представлены на рисунке. Поляризация длинноволнового перехода - XY.

4. (300) Кристалл кубического строения состоит из одинаковых абсолютно черных (поглощающих) молекул с радиусом R. Расстояние между молекулами L. Определить оптическую плотность такого кристалла толщиной 1 см при падении света перпендикулярно поверхности. Как измениться оптическая плотность при падении света под углом 45⁰?

Решение: Оптическая плотность изменяется от величин 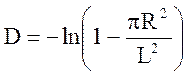 до .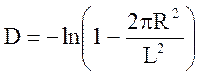

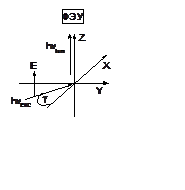
5. (400) Определить зависимость степени поляризации люминесценции от угла g в геометрии опыта, показанной на рисунке.

Решение: Поляризация равна нулю при любом угле g.

Решение задач на контрольной 18 апреля 2004 г. Группа 141-143

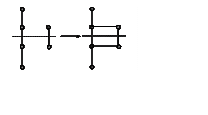
1. (300) Определить разрешенность по симметрии реакции присоединения H₄ + H₂®H₆. (см. рисунок). Построить корреляционную диаграмму и оценить изменение энергии в этой реакции. Считать все кулоновские интегралы для H₄ и H₆ одинаковыми.

Решение. Уровни энергии исходных молекул известны (Н₄ – бутадиеновая система). Для конечной молекулы Н₆ уровни легко найти, используя группу симметрии C_2v. В этом случае будут 2 детерминанта с корнями x = ±2.25, ±0.8, ±0.563. Корреляционная диаграмма показана на рисунке. Изменение энергии равно DE = 0.766b. Реакция разрешена термически.

2. (600) Определить количество различных частот, которые должны наблюдаться в КР спектре для циклической молекулы Н_n (n = 4k + 2) группы D_nh.

Решение. Если перемножить строчки характеров для тензора поляризуемости и колебательных функций, можно получить количество частот. Необходимо только учесть, что в разложении по НП для компонент тензора поляризуемости будет содержаться 2 полносимметричных представления, поэтому число частот необходимо уменьшить на единицу.

	E	2Cj	…	2C2kj	C2	(2k+1)C2’	(2k+1)C2’’	I	2Sj	…	2S2kj	sh	(2k+1)sv	(2k+1)sd
a	6	2cosmj(1+2cosmj)			2	2	2	6	2cosmj(-1+2cosmj)			2	2	2
Q	3N-6	-2(1+2cosmj)			2	0	2	0	0	0	0	N	2	0

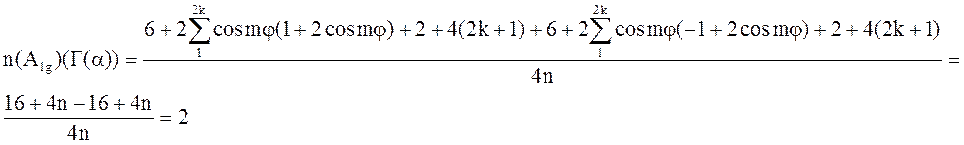
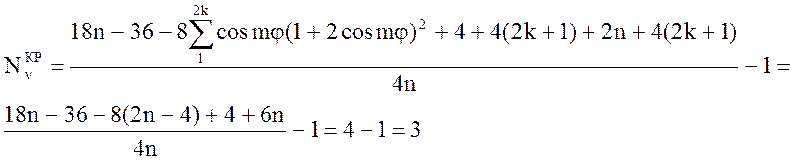
Таким образом, в КР спектре будут наблюдаться 3 частоты.

3. (400) Найти энергию d_z2 орбитали для иона с электронной конфигурацией d¹ в поле 8 зарядов, из которых 4 имеют заряд q, а 4 других 2q (см. рисунок). Все заряды расположены по сторонам квадрата.

Решение. Группа симметрии D_4h, в которой вложены друг в друга 2 квадрата. Результат можно просуммировать с учетом зарядов и расстояний.

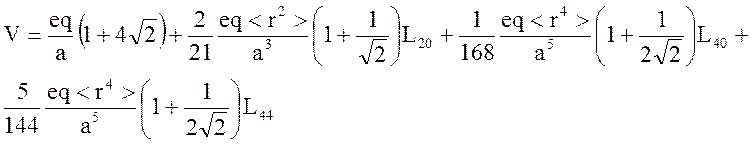
Таким образом, энергия d_z2 орбитали

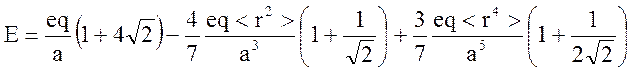
4. (400) Каждая молекула донора D связана с акцептором A1 молекулярным стержнем, и они находятся на расстоянии R₀, где R₀ – расстояние тушения по диполь-дипольному механизму. Время жизни возбужденного состояния свободного донора D 10^-6 сек. В раствор добавлен еще и другой тушитель A2 с концентрацией 10^-3 М. Определить константу бимолекулярного тушения донора D молекулой A2, если квантовый выход люминесценции донора уменьшился в 3 раза по сравнению со случаем отсутствия обоих тушителей (A1 и A2).

Решение. Для квантового выхода в этом случае можно написать выражение

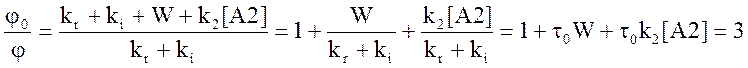
где

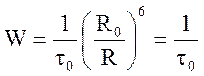
Таким образом,

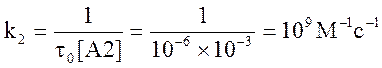
5. (300) Определить поляризацию и энергию переходов для молекулы H₄ с группой симметрии C_3v (см. рисунок).

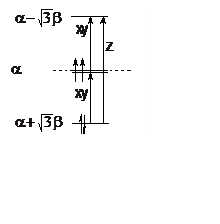Решение. В оптическом спектре этой молекулы будут две линии с энергиями  (поляризация xy) и  (поляризация z). Переходы показаны на рисунке.