Теория на экзамене 15 января 2001 года, группы 841, 842, 743
1. (400) Спин, спиновые функции, спиновые операторы. Определить спиновые состояния и спиновые функции для системы из двух одинаковых частиц со спином 1.
2. (400) Вырождение и термы электронных конфигураций. (в дополнение: найти вырождение и термы для l2 конфигурации в предположении, что у электронов нет спина (принцип Паули сохраняется).
3. (300) Спин-орбитальное расщепление. (в дополнение: проиллюстрировать на примере перехода p3 ® p2d1 (на сколько линий расщепляется переход между основными термами этих конфигураций в спектре, расстояния между линиями?)).
4. (400) Эффект Пашена-Бака (проиллюстрировать рассмотрением вопроса о том, на сколько уровней расщепится терм 2S+1L).
5. (500) Теория влияния заместителей на вырожденные орбитали в p-системах (определить в общем виде расщепление вырожденных орбиталей циклической p-системы, содержащей N центров и имеющей один индуктивный заместитель).
Задачи на экзамене 15 января 2001 года, группы 841, 842, 743
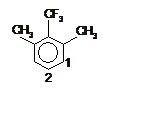 1. (200) Определить преимущественное
направление радикального замещения (центры 1 и 2) в молекуле
1,3-диметил-2-перфторметил-бензола (строение на рисунке).
1. (200) Определить преимущественное
направление радикального замещения (центры 1 и 2) в молекуле
1,3-диметил-2-перфторметил-бензола (строение на рисунке).
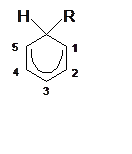 Решение: Отрежем индуктивные заместители и
присоединим радикал. Получим промежуточное состояние (рисунок), которое
находится на вершине барьера. Будем присоединять заместители к p-системе
пентильного радикала и спотреть изменение полной энергии этой системы, то есть
определять повышение или понижение барьера. При атаке радикала в первое
положение заместители присоединяем в 1, 2, 3 центры пентильного радикала.
Возмущение задается матричными элементами
Решение: Отрежем индуктивные заместители и
присоединим радикал. Получим промежуточное состояние (рисунок), которое
находится на вершине барьера. Будем присоединять заместители к p-системе
пентильного радикала и спотреть изменение полной энергии этой системы, то есть
определять повышение или понижение барьера. При атаке радикала в первое
положение заместители присоединяем в 1, 2, 3 центры пентильного радикала.
Возмущение задается матричными элементами
![]()
В соответствии с заселенностью и видом МО пентильного радикала изменение полной энергии равно
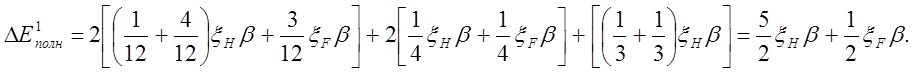
При атаке радикала во второе положение заместители присоединяем в 2, 3, 4 центры пентильного радикала. Возмущение задается матричными элементами
![]()
Изменение полной энергии в этом случае равно
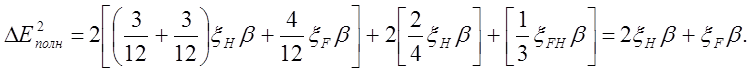
Так как xH = -0.1 и xF = 0.3, получим DE1полн = -0.1b и DE2полн = 0.1b. Учитывая отрицательное значение резонансного интеграла b, видим, что в первом случае барьер повышается, а во втором понижается, поэтому реакция по второму центру более предпочтительнее с энергетической точки зрения.
2. (500) Определить какому из термов электронной конфигурации p2 принадлежит функция
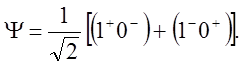
Напомним, что 1 и 0 обозначают проекции орбитального момента, а знаки + и – - проекции спина.
Решение: Легко показать, что для конфигурации p2 реализуются термы 3P, 1D и 1S. Все эти термы отличаются значением орбитального момента, поэтому принадлежность функции какому либо из них можно установить из уравнения
![]() .
.
Вспоминая определение оператора L2 через одноэлектронные операторы, можно раскрыть это уравнение
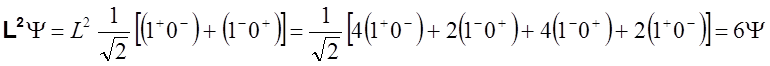
Таким образом, L(L+1) = 6 и L = 2, то есть функция принадлежит 1D терму.
3. (300) Определить расщепление (уровни энергии и вырождение) p2 конфигурации в очень сильном магнитном поле (считаем, что взаимодействие магнитных моментов с магнитным полем сильнее кулоновского отталкивания электронов, однако взаимодействие электронов с ядром больше магнитного взаимодействия).
Решение: Расщепление конфигурации определяется кулоновским отталкиванием электронов. Если магнитное взаимодействие больше, учитываем сначала его, то есть рассматриваем расщепление сразу конфигурации, а не термов. Спин орбитальное взаимодействие тоже считаем слабым. В этих условиях гамильтониан будет иметь вид
![]() ,
,
где H1 и H2 – гамильтонианы аналогичные гамильтониану атома водорода. Энергия p2 конфигурации задается этими операторами и будем считать ее за ноль энергии. Другие магнитные члены в гамильтониане будут давать энергию
![]()
Нетрудно подсчитать, что при mli = 1, 0, -1 и 2msi = 1, -1 эта формула определит 7 уровней энергии 3bН, 2bН, 1bН, 0bН, -1bН, -2bН, -3bН с вырождением 1, 2, 3, 3, 3, 2, 1 с суммарным вырождением 15, как это и должно быть для этой конфигурации.
4. (300) В тетраэдрической молекуле H4, в которой все атомы связаны между собой, рвется одна H-H связь. Определить изменение оптического спектра (указать энергии и поляризацию переходов в обоих случаях).
Решение: Для тетраэдра будут два уровня а1 (a+3b) и t2 (a-b), энергия перехода 4b с поляризацией x,y,z. После разрыва одной связи симметрия понижается до C2v. Легко показать, что будет существовать 4 молекулярных уровня 1а1 (a+2.561b), b2 (a), b1 (a-b), 2а1 (a-1.561b). Нижних по энергии два уровня полностью заселены, поэтому разрешенных будет 3 перехода b2 ® 2a1 (1.561b, y поляризация), 1a1 ® b1 (3.561b, x поляризация), 1a1 ® 2a1 (4.122b, z поляризация).
5. (400) Определить распределение спиновой плотности для анион-радикала нафталина по теории возмущений.
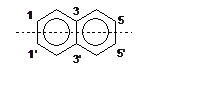 Решение: Если разрезать нафталин на два
пентадиенильных радикала, орбитали которых хорошо известны и ввести
взаимодействие центров, соответствующее молекуле нафталина, можно легко
определить, что на отмеченных центрах будет спиновая плотность 1/6.
Решение: Если разрезать нафталин на два
пентадиенильных радикала, орбитали которых хорошо известны и ввести
взаимодействие центров, соответствующее молекуле нафталина, можно легко
определить, что на отмеченных центрах будет спиновая плотность 1/6.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.