Контрольная 28 декабря 2000, группы 841, 842, 743
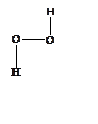 1. (600) При радиолизе раствора перекиси водорода
из-за ионизации молекул среды образуется плоский катион-радикал (Н2О2)+.
Определить основной терм этой частицы. Строение катион-радикала представлено на
рисунке.
1. (600) При радиолизе раствора перекиси водорода
из-за ионизации молекул среды образуется плоский катион-радикал (Н2О2)+.
Определить основной терм этой частицы. Строение катион-радикала представлено на
рисунке.
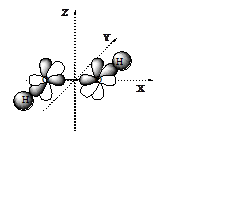 Решение: Группа симметрии этого катион-радикала C2h,
операции симметрии и таблица характеров которой представлена ниже
Решение: Группа симметрии этого катион-радикала C2h,
операции симметрии и таблица характеров которой представлена ниже
|
E |
C2 |
I |
sh |
|
|
Ag |
1 |
1 |
1 |
1 |
|
Au |
1 |
1 |
-1 |
-1 |
|
Bg |
1 |
-1 |
1 |
-1 |
|
Bu |
1 |
-1 |
-1 |
1 |
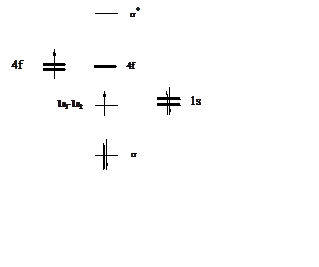 Анализ показывает, что комбинации с плюсом и минусом
орбиталей 2px атомов кислорода преобразуются по Ag и Bu представлениям, 2pz
атомов кислорода преобразуются по Au и Bg, 2py атомов кослорода преобразуются по Ag и Bu. Комбинации 1s орбиталей
атомов водорода со заками плюс и минус преобразуются по представлениям Ag и Bu, соответственно. Таким образом, 2pz образуют po-o и po-o*
орбитали, 2px - so-o и so-o*, а 2py вместе с 1s орбиталями атомов водорода – дважды вырожденные sO-H
и sO-H*.
Картинка уровней и распределение электронов представлены на рисунке.
Неспаренный электрон находится на po-o* орбитали, имеющей симметрию bg,
поэтому основной терм катион-радикала – 2Bg.
Анализ показывает, что комбинации с плюсом и минусом
орбиталей 2px атомов кислорода преобразуются по Ag и Bu представлениям, 2pz
атомов кислорода преобразуются по Au и Bg, 2py атомов кослорода преобразуются по Ag и Bu. Комбинации 1s орбиталей
атомов водорода со заками плюс и минус преобразуются по представлениям Ag и Bu, соответственно. Таким образом, 2pz образуют po-o и po-o*
орбитали, 2px - so-o и so-o*, а 2py вместе с 1s орбиталями атомов водорода – дважды вырожденные sO-H
и sO-H*.
Картинка уровней и распределение электронов представлены на рисунке.
Неспаренный электрон находится на po-o* орбитали, имеющей симметрию bg,
поэтому основной терм катион-радикала – 2Bg.
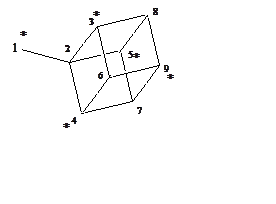
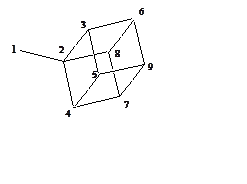 2. (400) Найти распределение спиновой плотности для
радикала Н9, строение которого показано на рисунке.
2. (400) Найти распределение спиновой плотности для
радикала Н9, строение которого показано на рисунке.
Решение: Этот радикал является нечетной альтернантной системой, поэтому неспаренный электрон находится на орбитали с энергией E = a (x = 0). Группа симметрии радикала – C3v. Очевидно, что по полносимметричному представлению будут преобразовываться комбинации орбиталей
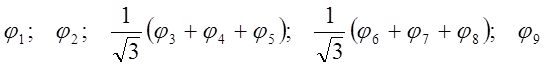
 Для этих 5 функций детерминант, умноженный на столбец
из коэффициентов будет иметь вид
Для этих 5 функций детерминант, умноженный на столбец
из коэффициентов будет иметь вид
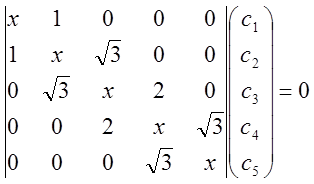
Для
x = 0 получим уравнения с2 = с4
= 0, 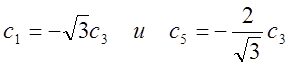 . Отсюда получаем значения
. Отсюда получаем значения 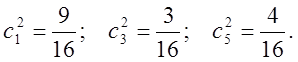 Спиновая плотность получается
Спиновая плотность получается
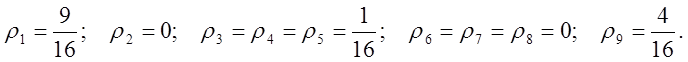
Таким образом, спиновая плотность действительно находится только на "звездчатых" центрах 1, 3-5, 9.
3. (200) Определить основной терм линейной молекулы H-Ce3+-H.
 Решение: Электронная конфигурация иона Ce3+ - 4f1.
Орбиталь 4f0 (0 –
проекция орбитального момента) будет взаимодействовать с комбинацией
Решение: Электронная конфигурация иона Ce3+ - 4f1.
Орбиталь 4f0 (0 –
проекция орбитального момента) будет взаимодействовать с комбинацией 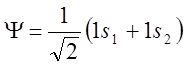 , давая связывающую и разрыхляющую орбитали
(s и s*). Орбитали 4f±3, 4f±2, 4f±1 и
комбинация
, давая связывающую и разрыхляющую орбитали
(s и s*). Орбитали 4f±3, 4f±2, 4f±1 и
комбинация 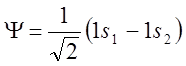 остануться несвязывающими. Таким образом,
картинка МО будет выглядеть, как показано на рисунке и терм будет 2Su+.
остануться несвязывающими. Таким образом,
картинка МО будет выглядеть, как показано на рисунке и терм будет 2Su+.
4. (300) Две одинаковые циклические p-системы с N центрами каждая обьединяются в одну общую циклическую p-систему с 2N центрами (N = 4k+2). Определить изменение полной p-электронной энергии при таком объединении.
Решение: Энергия молекулярных орбиталей для циклических p-систем определяется выражением
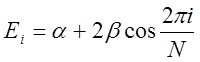
Для случая N = 4k+2 верхняя занятая 4 электронами МО имеет номер i = k = (N-2)/4. В этой ситуации полная электронная энергия равна
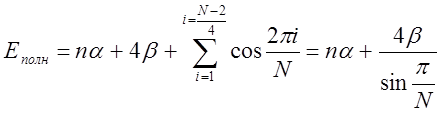 . Для двух одинаковых p-систем полная энергия
. Для двух одинаковых p-систем полная энергия
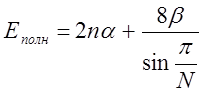 . После объединения двух систем в одну
количество центров удваивается и 2N = 2(2k+2) = 4k+4 =
4k'. Для такой системы на высших двух вырожденных
орбиталях с i = N/2 находится только 2 электрона, на предшествующих
двух орбиталях с i = (2N-4)/4 находится 4 электрона. Полная электронная
энергия в этом случае
. После объединения двух систем в одну
количество центров удваивается и 2N = 2(2k+2) = 4k+4 =
4k'. Для такой системы на высших двух вырожденных
орбиталях с i = N/2 находится только 2 электрона, на предшествующих
двух орбиталях с i = (2N-4)/4 находится 4 электрона. Полная электронная
энергия в этом случае
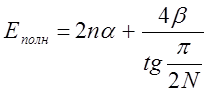 . Таким образом, изменение энергии после
объединения систем
. Таким образом, изменение энергии после
объединения систем
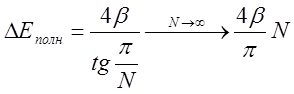
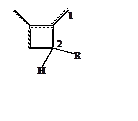
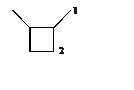 5. (500) Для p-системы, строение
которой представлено на рисунке определить более предпочтительное направление
радикального замещения по центрам 1 или 2 (неэквивалентность центров задается
геометрией молекулы). Отметим, что в этой молекуле центры 1 не заместители, а
группы CH2 с p-центрами.
5. (500) Для p-системы, строение
которой представлено на рисунке определить более предпочтительное направление
радикального замещения по центрам 1 или 2 (неэквивалентность центров задается
геометрией молекулы). Отметим, что в этой молекуле центры 1 не заместители, а
группы CH2 с p-центрами.
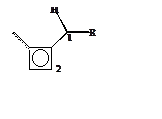
 Решение: Оставшаяся p-система
промежуточного состояния с присоединенным радикалом в обоих случаях показана на
рисунке. Определив энергии МО, легко подсчитать, что энергия оставшейся p-системы при радикальном замещении по 1 центру равна E(1)
= 5a + 5.596b, а по второму E(2)
= 5a + 6.324b. Таким образом, во
втором случае энергия оставшейся p-системы ниже и 2
центр является более предпочтительным при радикальном замещении.
Решение: Оставшаяся p-система
промежуточного состояния с присоединенным радикалом в обоих случаях показана на
рисунке. Определив энергии МО, легко подсчитать, что энергия оставшейся p-системы при радикальном замещении по 1 центру равна E(1)
= 5a + 5.596b, а по второму E(2)
= 5a + 6.324b. Таким образом, во
втором случае энергия оставшейся p-системы ниже и 2
центр является более предпочтительным при радикальном замещении.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.