Критерий устойчивости Найквиста [1].
Передаточная функция разомкнутой системы:
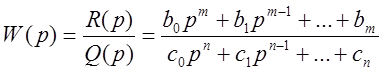 .
.
Причём степень числителя не может
быть больше степени знаменателя, ![]() .
.
Частотная
передаточная функция получается при подстановке ![]() :
:
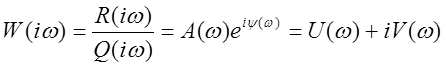 .
.
Уточним смысл частотной передаточной функции. Система управления в разомкнутом состоянии:
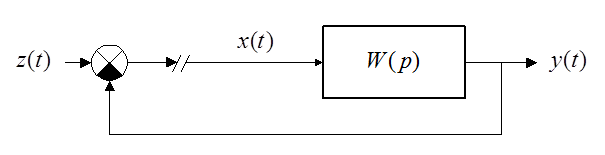 .
.
Если на вход
звена ![]() подать гармонический сигнал ошибки
подать гармонический сигнал ошибки ![]() с амплитудой
с амплитудой ![]() , то в
установившемся режиме величина
, то в
установившемся режиме величина ![]() на выходе будет также
изменяться по гармоническому закону с амплитудой
на выходе будет также
изменяться по гармоническому закону с амплитудой ![]() и
фазовым сдвигом
и
фазовым сдвигом ![]() . Модуль частотной передаточной
характеристики представляет собой отношение амплитуд выходной и входной величин
. Модуль частотной передаточной
характеристики представляет собой отношение амплитуд выходной и входной величин
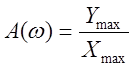 ,
,
а аргумент – сдвиг фазы ![]() .
.
Если изменять частоту
входного сигнала от ![]() до
до ![]() и
откладывать на комплексной плоскости точки, соответствующие получающимся
комплексным числам, то геометрическое место этих точек образует
амплитудно-фазовую характеристику разомкнутой системы (АФХ).
и
откладывать на комплексной плоскости точки, соответствующие получающимся
комплексным числам, то геометрическое место этих точек образует
амплитудно-фазовую характеристику разомкнутой системы (АФХ).
В реальных
системах всегда ![]() . Поэтому при
. Поэтому при ![]() , модуль частотной передаточной функции
стремится к нулю и соответствующая точка попадает в начало координат.
, модуль частотной передаточной функции
стремится к нулю и соответствующая точка попадает в начало координат.
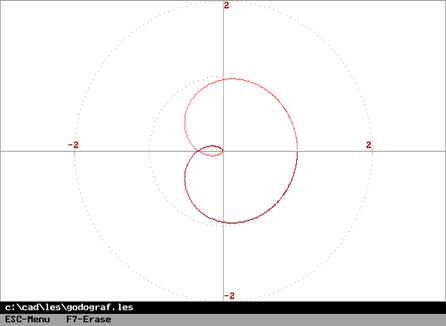
Сформулируем необходимые и достаточные требования к АФХ разомкнутой системы, при выполнении которых система будет устойчивой в замкнутом состоянии.
Статическая система.
Рассмотрим
вначале статическую систему, т.е. такую, знаменатель передаточной
функции которой ![]() не имеет в качестве сомножителя
оператор p. Кроме того, рассмотрим пока только
устойчивые в разомкнутом состоянии системы, т.е. такие, полюсы
не имеет в качестве сомножителя
оператор p. Кроме того, рассмотрим пока только
устойчивые в разомкнутом состоянии системы, т.е. такие, полюсы ![]() которых (иначе – нули
которых (иначе – нули ![]() ) лежат в левой полуплоскости.
) лежат в левой полуплоскости.
Введём вспомогательную функцию (заметим, что это знаменатель передаточной функции замкнутой системы)
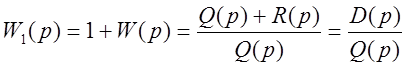 .
.
Числитель ![]() является
знаменателем передаточной функции замкнутой системы и, в силу этого,
представляет собой характеристический полином замкнутой системы.
Соответствующий характеристический комплекс:
является
знаменателем передаточной функции замкнутой системы и, в силу этого,
представляет собой характеристический полином замкнутой системы.
Соответствующий характеристический комплекс:
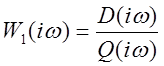 .
.
Результирующий угол поворота
вектора ![]() при изменении частоты от
при изменении частоты от ![]() до
до ![]()
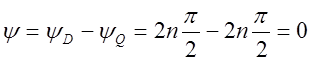 ,
,
так как устойчивы замкнутая и
разомкнутая системы (все корни уравнения ![]() и
уравнения
и
уравнения ![]() лежат в левой полуплоскости) – критерий
Михайлова.
лежат в левой полуплоскости) – критерий
Михайлова.
Итак, если система с
передаточной функцией ![]() устойчива в замкнутом состоянии,
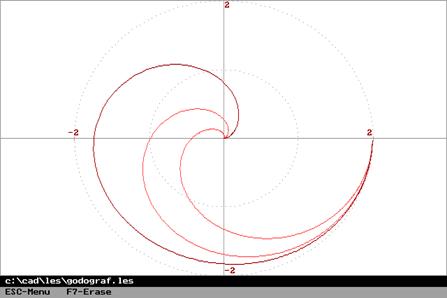
то годограф
устойчива в замкнутом состоянии,
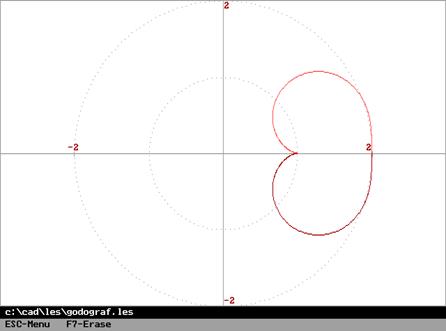
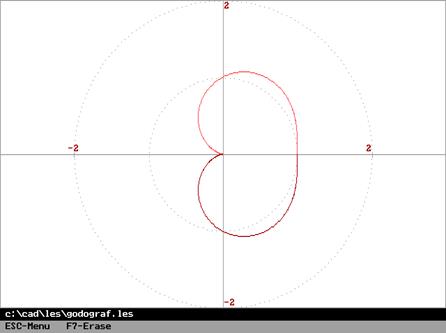
то годограф ![]() не охватывает начало координат
(необходимость). И наоборот, если годограф
не охватывает начало координат
(необходимость). И наоборот, если годограф ![]() не
охватывает начало координат, или, что то же самое, годограф
не
охватывает начало координат, или, что то же самое, годограф ![]() не охватывает точку с координатами (
не охватывает точку с координатами (![]() ), то система устойчива в замкнутом
состоянии (достаточность).
), то система устойчива в замкнутом
состоянии (достаточность).
Доказательство достаточности.
Коль скоро ![]() , и нули
, и нули ![]() лежат в
левой полуплоскости, то
лежат в
левой полуплоскости, то 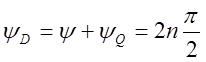 . Таким образом,
согласно критерию Михайлова, все нули
. Таким образом,
согласно критерию Михайлова, все нули ![]() лежат в
левой полуплоскости, т.е. замкнутая система устойчива.
лежат в
левой полуплоскости, т.е. замкнутая система устойчива.
Различают случаи абсолютно устойчивой системы, условно устойчивой системы, случай нахождения системы на границе устойчивости (колебательная устойчивость) и случай неустойчивой системы.
Абсолютно устойчивая система остаётся устойчивой при любом уменьшении коэффициента усиления разомкнутой цепи. Условно устойчивая система будет устойчивой при изменении коэффициента усиления в определённых пределах.
Если система находится
на границе устойчивости, то это будет устойчивость колебательного типа. В самом
деле, коль скоро при некоторой частоте годограф пересекает точку с координатами
(![]() ), то
), то
![]() , или
, или ![]() .
.
Т.е. чисто мнимый корень является решением характеристического уравнения.
Система с астатизмом первого порядка.
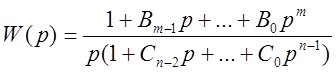 .
.
Пусть все нули
знаменателя (кроме ![]() ) лежат в левой полуплоскости.
Т.е. в разомкнутом состоянии система является нейтрально устойчивой.
) лежат в левой полуплоскости.
Т.е. в разомкнутом состоянии система является нейтрально устойчивой.
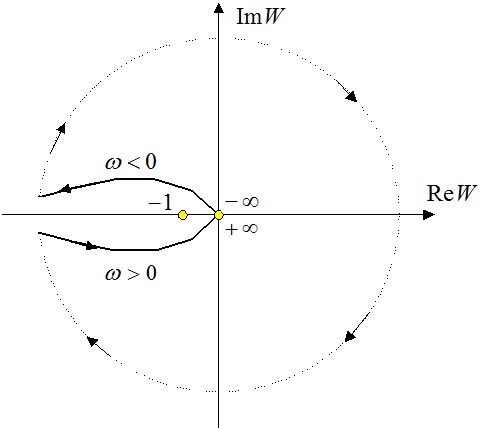
Амплитудно-фазовая
характеристика имеет разрыв в точке ![]() . Модуль стремится к
бесконечности, а фаза испытывает скачок на
. Модуль стремится к
бесконечности, а фаза испытывает скачок на ![]() . При
изменении частоты от
. При
изменении частоты от ![]() до
до ![]() изображающая
точка движется снизу вверх по мнимой оси.
изображающая
точка движется снизу вверх по мнимой оси.
Для
получения определённости в ходе амплитудно-фазовой характеристики необходимо
отнести нулевой корень знаменателя передаточной функции ![]() либо
к левой, либо к правой полуплоскости корней. Первое является более удобным, так
как при этом все корни знаменателя
либо
к левой, либо к правой полуплоскости корней. Первое является более удобным, так
как при этом все корни знаменателя ![]() будут расположены в
левой полуплоскости [1, с.154].
будут расположены в
левой полуплоскости [1, с.154].
Обойдём нашу точку справа по полуокружности бесконечно малого радиуса. При этом передаточная функция
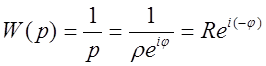 .
.
Здесь ![]() , а
аргумент (
, а
аргумент (![]() ) меняется в пределах от
) меняется в пределах от ![]() до
до ![]() .
.
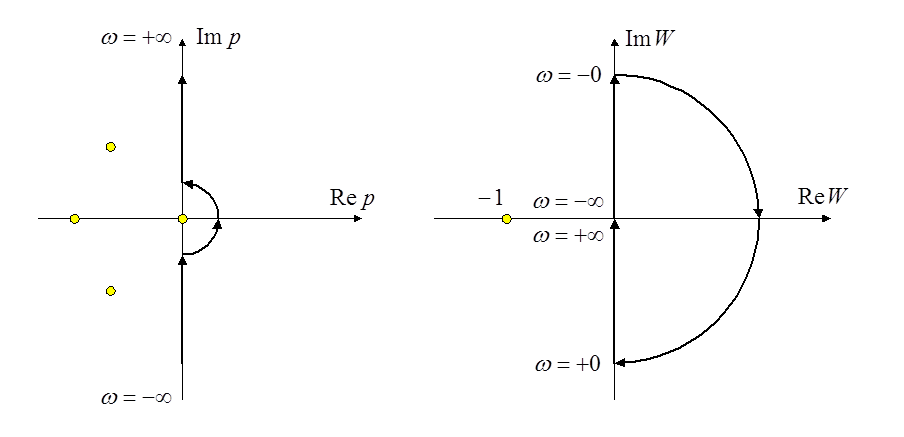
Таким образом, во время
движения по полуокружности бесконечно малого радиуса передаточная функция может
быть представлена в виде вектора бесконечно большой длины, поворачивающегося на
комплексной плоскости по часовой стрелке на угол, равный ![]() (от
(от ![]() до
до ![]() ), что соответствует полуокружности
бесконечно большого радиуса. Характеристика не охватывает точку (
), что соответствует полуокружности
бесконечно большого радиуса. Характеристика не охватывает точку (![]() ), и система в замкнутом состоянии будет
устойчивой.
), и система в замкнутом состоянии будет
устойчивой.
В принципе такая система может быть абсолютно, условно или колебательно устойчивой, а также неустойчивой.
Система с астатизмом второго порядка.
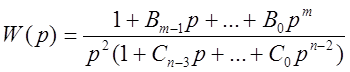 .
.
При обходе двойного нулевого корня в начале
координат передаточная функция разомкнутой системы может быть представлена
вектором бесконечно большой длины, поворачивающимся по часовой стрелке на угол ![]() .
.
Такая система также может быть абсолютно, условно или колебательно устойчивой, а также неустойчивой.
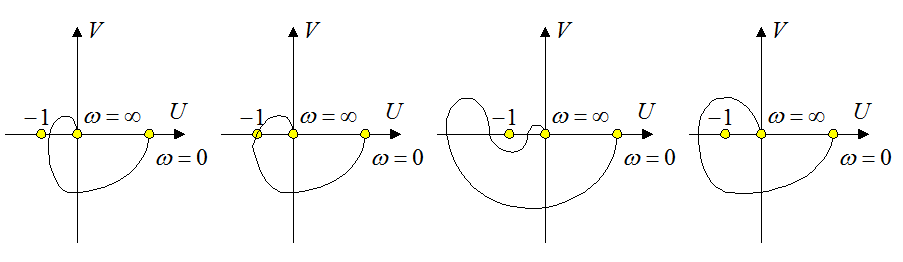
В принципе, для определения устойчивости системы с астатизмом любого порядка, достаточно построить ветвь амплитудно-фазовой характеристики только для положительных частот, дополнив её окружностью бесконечно большого радиуса, как это изображено на рисунке ниже.
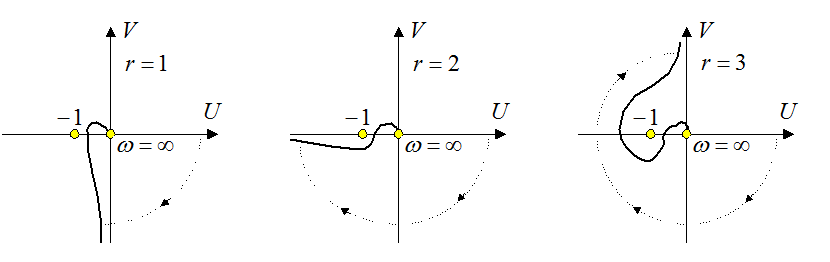
Из рисунка, в
частности, следует, что абсолютная устойчивость может быть получена при степени
астатизма ![]() . При большей степени астатизма может быть
получена только условная устойчивость.
. При большей степени астатизма может быть
получена только условная устойчивость.
Критерий Найквиста в общем случае.
Пусть
знаменатель ![]() передаточной функции разомкнутой системы
передаточной функции разомкнутой системы ![]() с любой степенью астатизма содержит корни,
лежащие в правой полуплоскости. Это соответствует неустойчивой в разомкнутом
состоянии системе. Возможные причины неустойчивости: наличие неустойчивых
звеньев или звеньев неустойчивых вследствие внутренней обратной связи.
с любой степенью астатизма содержит корни,
лежащие в правой полуплоскости. Это соответствует неустойчивой в разомкнутом
состоянии системе. Возможные причины неустойчивости: наличие неустойчивых
звеньев или звеньев неустойчивых вследствие внутренней обратной связи.
Замкнутая
система может быть как устойчивой, так и неустойчивой. При этом несколько
меняется критерий Найквиста: замкнутая система будет устойчивой, если
при изменении частоты от ![]() до
до ![]() результирующий угол поворота годографа
вектора
результирующий угол поворота годографа
вектора ![]() относительно точки (
относительно точки (![]() ) будет равен
) будет равен ![]() , где l – число корней полинома
, где l – число корней полинома ![]() лежащих
в правой полуплоскости.
лежащих
в правой полуплоскости.
Для доказательства введём вспомогательную функцию (заметим, что это знаменатель передаточной функции замкнутой системы)
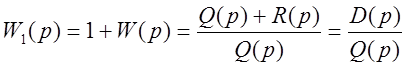 .
.
Таким образом, числитель ![]() – характеристический полином замкнутой
системы. Соответствующий характеристический комплекс:
– характеристический полином замкнутой
системы. Соответствующий характеристический комплекс:
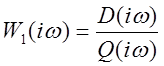 .
.
Если система
устойчива в замкнутом состоянии, то результирующий угол поворота вектора ![]() при изменении частоты от
при изменении частоты от ![]() до
до ![]()
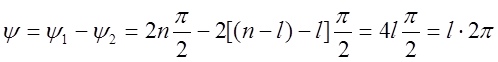 .
.
Иначе, годограф
![]() l раз
обойдёт точку (
l раз
обойдёт точку (![]() ) против часовой стрелки.
) против часовой стрелки.
Для того чтобы
воспользоваться этим критерием, необходимо знать, сколько корней у знаменателя
передаточной функции лежат в правой полуплоскости. Для этого прежде надо
исследовать соответствующий полином ![]() .
.
Хотя теоретически система в замкнутом состоянии может быть устойчивой при наличии неустойчивости по цепи местной обратной связи, практически такой случай является нежелательным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.