Многоконтурная система обратной связи

Многоконтурная система обратной связи.

          Размыкание многоконтурной системы обратной связи с целью получения передаточной функции можно делать в произвольном месте.

Размыкание b/a на входе первого звена (для получения главной передаточной функции):

.

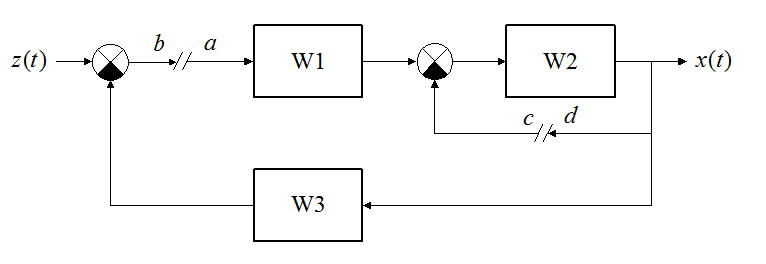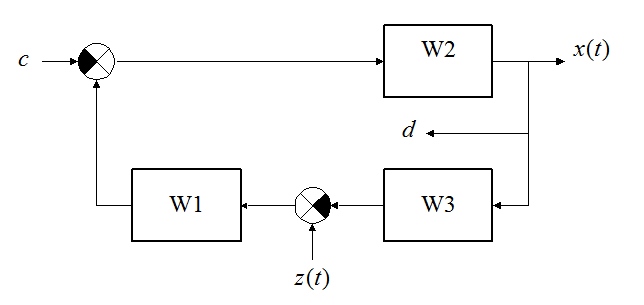
Передаточная функция (главная):

.

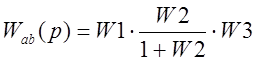Размыкание c/d:

.

Передаточная функция:

.

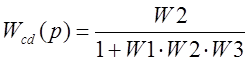Передаточные функции различны. Тем не менее, характеристические уравнения замкнутой системы одинаковы:

,

.

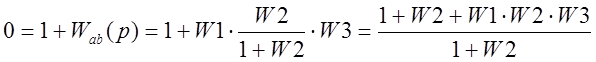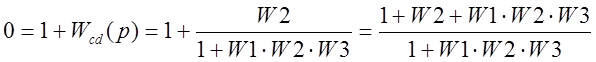Таким образом, для определения устойчивости, можно пользоваться передаточной функцией системы, полученной размыканием исходной системы в произвольной точке. Однако только главная передаточная функция связана с передаточной функцией замкнутой системы известным соотношением:

.

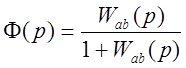Из того обстоятельства, что при исследовании устойчивости замкнутой системы нас интересует только характеристическое уравнение

,

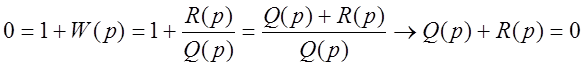следует, что для расчёта устойчивости может быть использована преобразованная передаточная функция

,

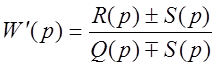где  – произвольный полином степени меньшей, чем степень полинома , т.к.

.

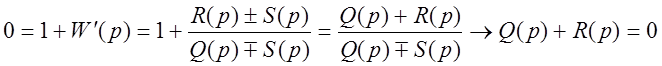Многомерные системы регулирования [1].

          К многомерным относятся системы, имеющие несколько регулируемых величин:

, ().

Многомерный объект управления описывается системой уравнений, обычно представляемой в матричной форме:

, , .

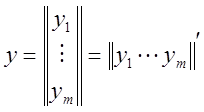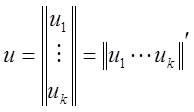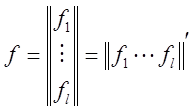Здесь u, f – управляющие и возмущающие воздействия (векторы).

          Уравнения движения в матричной форме:

.

Здесь

, ,

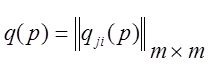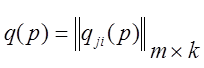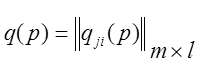
 – квадратная и прямоугольные матрицы операторных коэффициентов.

          Для изображений по Лапласу (при нулевых начальных условиях):

.

Здесь , ,  – матрицы-столбцы изображений регулируемых величин, управляющих величин и возмущений.

Если определитель , то существует обратная матрица 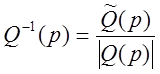. Умножая исходное уравнение слева на  получим:

, где ,

 – матрицы передаточных функций объекта для управляющих величин и возмущений.

Путём нахождения обратного преобразования Лапласа для каждого элемента матриц передаточных функций объекта получается так называемая матрица Коши (матрица весовых функций). Например, для управляющих воздействий

.

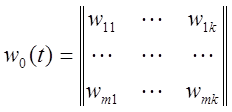          Если в момент времени  на все входы поступают управляющие воздействия , где , то изменение j-той регулируемой величины записывается посредством интеграла Дюамеля-Карстона:

.

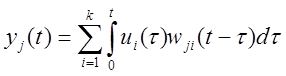На рисунке ниже изображена структурная схема замкнутой многомерной системы автоматического регулирования. Она в точности такая же, как схема одномерной системы, только g, x, u, y, f здесь векторы, а , ,  – матрицы.

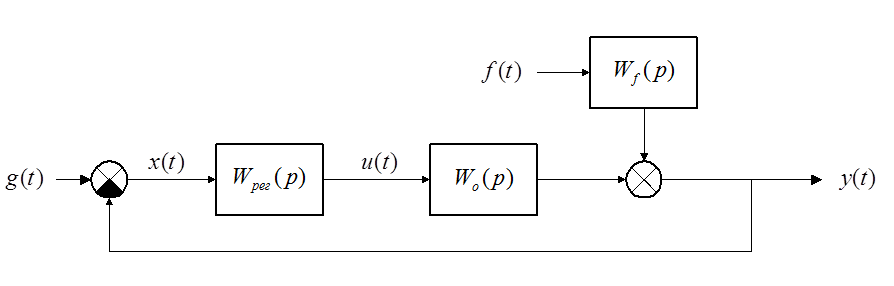
Матрица передаточных функций разомкнутой по всем каналам системы:

.

Характеристическая матрица системы – квадратная матрица размером , E – единичная матрица:

.

Характеристическое уравнение – определитель характеристической матрицы:

.

Матрицы передаточных функций замкнутой системы, замкнутой системы по ошибке и замкнутой системы по возмущениям:

, , .

Устойчивость двухмерной системы с антисимметричными связями.

          Структурная схема двухканальной системы слежения:

.

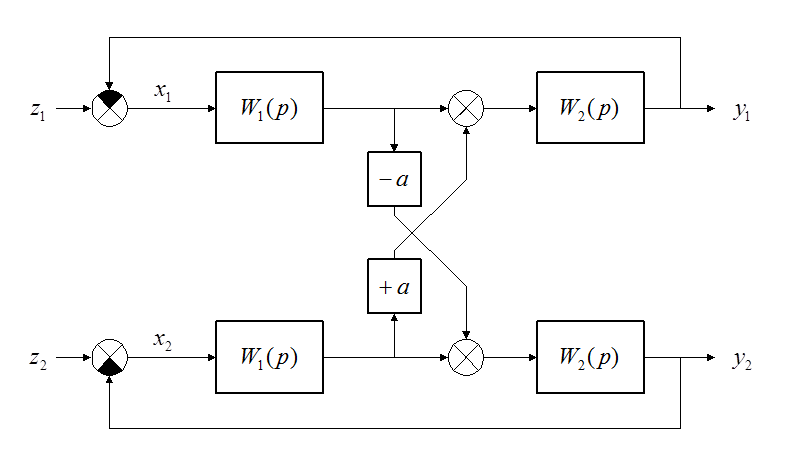Связь выходных (регулируемых) величин с ошибками:

.

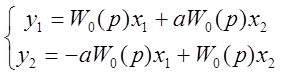Здесь .

Матричная запись:

.

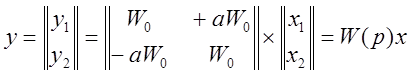Характеристическое уравнение:

.

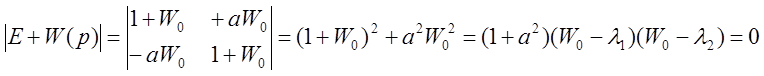Здесь

.

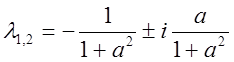Исследование устойчивости сводится к рассмотрению двух уравнений:

 и .

Здесь может быть использован критерий Найквиста, но вместо точки комплексной плоскости (), которая соответствует обычной записи характеристического уравнения , необходимо рассматривать две точки, соответствующие комплексным числам  и .

Замкнутая система будет устойчивой, если АФХ устойчивого в разомкнутом состоянии одного изолированного канала не будет охватывать точек  и .

          Колебательная граница устойчивости будет иметь место, если выполняется одно из равенств  или .

Заметим, что при  обе точки  и  стягиваются в точку , что соответствует обычной формулировке критерия Найквиста.

.

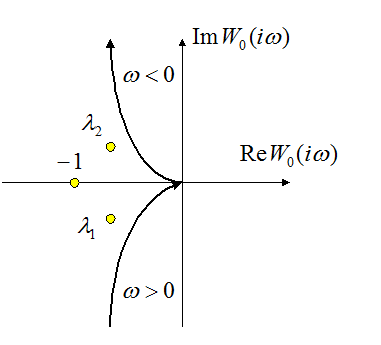Другой метод расчёта устойчивости двухмерной системы.

Введём , , . Были соотношения:

.

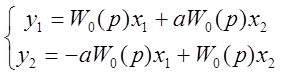Умножим второе равенство на i и сложим:

.

Здесь  – эквивалентная передаточная функция разомкнутой двухмерной системы,  – угол поворота передаточной функции  по часовой стрелке,  – коэффициент увеличения модуля .

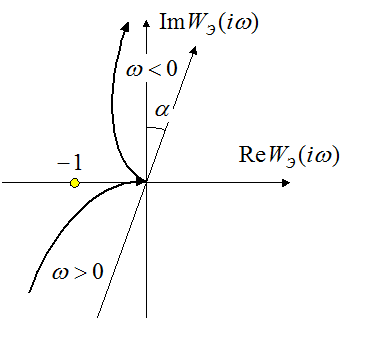
Колебательная граница устойчивости: , что сводится к

.

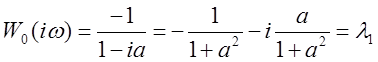Это согласуется с первым методом расчёта устойчивости.