Критерий устойчивости Найквиста [2].
Передаточная
функция стационарной линейной системы ![]() приводит
в соответствие каждому значению её аргумента
приводит
в соответствие каждому значению её аргумента ![]() комплексное
число
комплексное
число ![]() , которое может быть изображено на
комплексной плоскости
, которое может быть изображено на
комплексной плоскости ![]() .
.
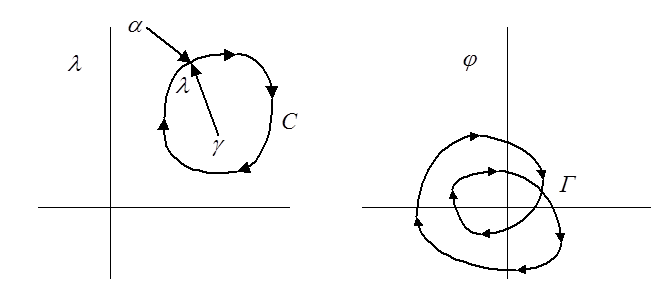
В частности,
амплитудно-фазовая характеристика системы ![]() является
отображением мнимой оси плоскости переменной
является
отображением мнимой оси плоскости переменной ![]() .
.
Пусть точка ![]() описывает кривую С по ходу часовой
стрелки. Для любой точки
описывает кривую С по ходу часовой
стрелки. Для любой точки ![]() , лежащей вне области,
ограниченной кривой С, изменение аргумента комплексного числа
, лежащей вне области,
ограниченной кривой С, изменение аргумента комплексного числа ![]() равно нулю. Напротив, для любой точки
равно нулю. Напротив, для любой точки ![]() , лежащей внутри этой области, вектор,
изображающий комплексное число
, лежащей внутри этой области, вектор,
изображающий комплексное число ![]() , поворачивается по
часовой стрелке на угол
, поворачивается по
часовой стрелке на угол ![]() (при этом аргумент
комплексного числа
(при этом аргумент
комплексного числа ![]() изменяется на
изменяется на ![]() ).
).
Пусть функция ![]() не имеет на кривой С ни нулей, ни
полюсов, а внутри области имеет h нулей и l полюсов:
не имеет на кривой С ни нулей, ни
полюсов, а внутри области имеет h нулей и l полюсов:
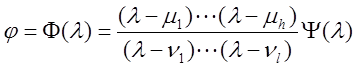 .
.
При обходе
точкой ![]() кривой С по часовой стрелке аргумент
числителя получает приращение
кривой С по часовой стрелке аргумент
числителя получает приращение ![]() , а знаменателя
, а знаменателя ![]() . Таким образом, точка
. Таким образом, точка ![]() обходит начало координат по часовой
стрелке
обходит начало координат по часовой
стрелке ![]() раз (аргумент
раз (аргумент ![]() изменяется
на
изменяется
на ![]() ).
).
Передаточная функция замкнутой стационарной линейной системы имеет вид:
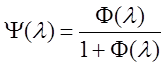 .
.
Пусть
разомкнутая система устойчива, т.е. ![]() не имеет полюсов в
правой полуплоскости и на мнимой оси. Для устойчивости замкнутой системы
необходимо и достаточно, чтобы знаменатель
не имеет полюсов в
правой полуплоскости и на мнимой оси. Для устойчивости замкнутой системы
необходимо и достаточно, чтобы знаменатель ![]() не имел
нулей в правой полуплоскости и на мнимой оси. Очевидно, что началу координат
плоскости переменной
не имел
нулей в правой полуплоскости и на мнимой оси. Очевидно, что началу координат
плоскости переменной ![]() соответствует точка
соответствует точка ![]() плоскости переменной
плоскости переменной ![]() .
.
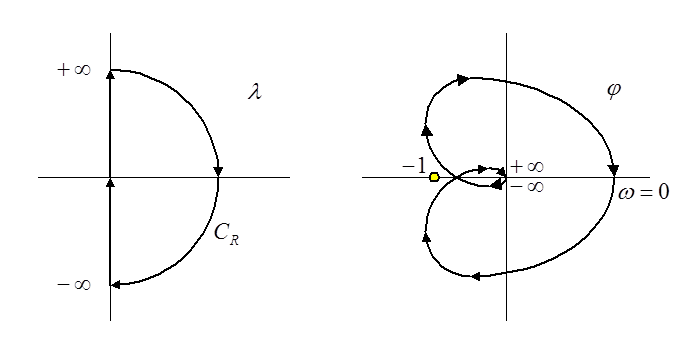
Возьмём на
плоскости переменной ![]() контур
контур ![]() ,
состоящий из отрезка мнимой оси (
,
состоящий из отрезка мнимой оси (![]() ) и полуокружности
большого радиуса R, лежащей в правой
полуплоскости. Так как при любом R функция
) и полуокружности
большого радиуса R, лежащей в правой
полуплоскости. Так как при любом R функция ![]() , а следовательно, и функция
, а следовательно, и функция ![]() не имеет полюсов на контуре
не имеет полюсов на контуре ![]() и в соответствующем полукруге, то при
обходе точкой
и в соответствующем полукруге, то при
обходе точкой ![]() этого контура точка
этого контура точка ![]() обходит точку
обходит точку ![]() по ходу
часовой стрелки столько раз, сколько нулей имеет функция
по ходу
часовой стрелки столько раз, сколько нулей имеет функция ![]() в этом полукруге.
в этом полукруге.
Итак, в случае
устойчивой разомкнутой системы для устойчивости замкнутой системы необходимо и
достаточно, чтобы амплитудно-фазовая характеристика разомкнутой системы не
охватывала точку ![]() и не проходила через неё.
и не проходила через неё.
Случай неустойчивой разомкнутой системы.
Пусть
передаточная функция разомкнутой системы ![]() имеет k полюсов в правой полуплоскости и не имеет полюсов на
мнимой оси. В этом случае функция
имеет k полюсов в правой полуплоскости и не имеет полюсов на
мнимой оси. В этом случае функция ![]() также имеет k полюсов в правой полуплоскости. Следовательно, чтобы
функция
также имеет k полюсов в правой полуплоскости. Следовательно, чтобы
функция ![]() не имела нулей в правой полуплоскости,
необходимо и достаточно, чтобы кривая
не имела нулей в правой полуплоскости,
необходимо и достаточно, чтобы кривая ![]() обходила
точку
обходила
точку ![]() против часовой стрелки k раз (наличие нулей привело бы к соответствующему
уменьшению этого числа).
против часовой стрелки k раз (наличие нулей привело бы к соответствующему
уменьшению этого числа).
Полюсы на мнимой оси.
Если
передаточная функция разомкнутой системы имеет полюсы на мнимой оси, то контур
в плоскости ![]() следует деформировать таким образом, чтобы
обойти полюсы, лежащие на мнимой оси, по полуокружностям малого радиуса. Так
как разомкнутая система в этом случае неустойчива, то мы условимся обходить эти
полюсы слева, т.е. относить их к правой полуплоскости [2, с.202].
следует деформировать таким образом, чтобы
обойти полюсы, лежащие на мнимой оси, по полуокружностям малого радиуса. Так
как разомкнутая система в этом случае неустойчива, то мы условимся обходить эти
полюсы слева, т.е. относить их к правой полуплоскости [2, с.202].
Лирическое отступление.
Напомним что
авторы [1, Бесекерский и Попов] (в отличие от только что цитированного выше
автора [2, Пугачёв]) не квалифицируют полюс типа ![]() как
признак неустойчивости разомкнутой системы, относят его к левой полуплоскости и
обходят, естественно, справа.
как
признак неустойчивости разомкнутой системы, относят его к левой полуплоскости и
обходят, естественно, справа.
Замечательно, однако, то, что вид критерия устойчивости Найквиста не зависит от способа обхода.
Если, по-вашему,
корни на мнимой оси не свидетельствуют о неустойчивости разомкнутой системы, то
обходите их справа. При этом соответствующая полуокружность большого радиуса
обходит начало координат плоскости ![]() по часовой стрелке
справа, и точка
по часовой стрелке
справа, и точка ![]() не охватывается кривой. Как и
должно быть, в случае устойчивой в разомкнутом состоянии системы, чтобы
замкнутая система была устойчивой.
не охватывается кривой. Как и
должно быть, в случае устойчивой в разомкнутом состоянии системы, чтобы
замкнутая система была устойчивой.
Если же, по-вашему,
корни на мнимой оси свидетельствуют о неустойчивости разомкнутой системы, то
обходите их слева. При этом соответствующая полуокружность большого радиуса
обходит начало координат плоскости ![]() против часовой стрелке
слева, и точка
против часовой стрелке
слева, и точка ![]() охватывается годографом столько
раз, сколько корней вы отнесли к правой полуплоскости. Как и должно быть, в
случае неустойчивой в разомкнутом состоянии системы, чтобы замкнутая система
была устойчивой.
охватывается годографом столько
раз, сколько корней вы отнесли к правой полуплоскости. Как и должно быть, в
случае неустойчивой в разомкнутом состоянии системы, чтобы замкнутая система
была устойчивой.
Покажем это на следующем примере (система стабилизации радиального положения пучка протонного синхротрона ТРАПП, ИЯФ).
Пусть передаточная функция разомкнутой системы имеет три полюса на мнимой оси:
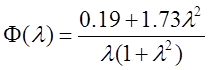 .
.
Отнесём эти полюсы к левой
полуплоскости (передаточная функция ![]() ) или правой
полуплоскости (передаточная функция
) или правой
полуплоскости (передаточная функция ![]() ) не мысленно, а явным
образом:
) не мысленно, а явным
образом:
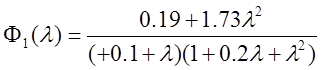 ,
, 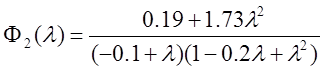 .
.
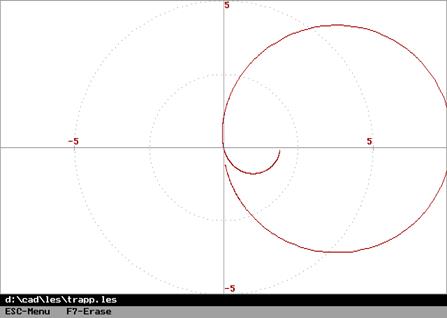
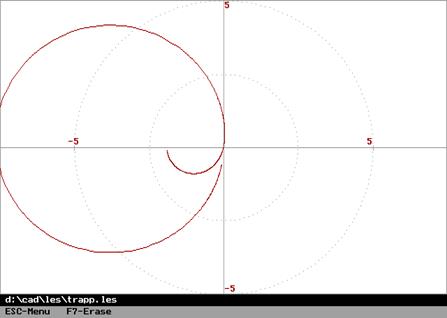
Ниже на рисунке изображены соответствующие годографы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.