Метод припасовывания.
Часто нелинейные системы представляются как кусочно-линейные, т.е. их динамика описывается линейными дифференциальными уравнениями, разными для разных участков процесса управления.
Метод припасовывания состоит в том, что линейные дифференциальные уравнения решаются в общем виде для каждого участка процесса, на котором они справедливы. Затем произвольные постоянные определяются таким образом, чтобы сшить эти участки. Значения фазовых координат в конце каждого участка служат начальными условиями для следующего участка.
Метод припасовывания применим и тогда, когда какой-либо участок описывается нелинейным дифференциальным уравнением, если известно его общее решение.
Пример.Структурная схема системы и нелинейная характеристика регулятора:
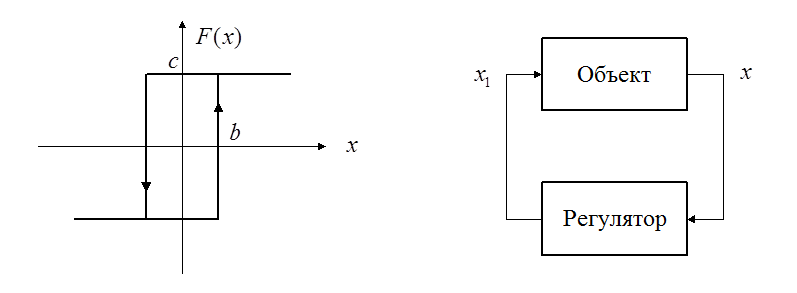
Уравнение движение объекта и уравнение регулятора:
![]() ,
, ![]() .
.
Общее уравнение замкнутой системы:
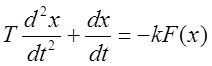 .
.
Возможный качественный вид переходного процесса:
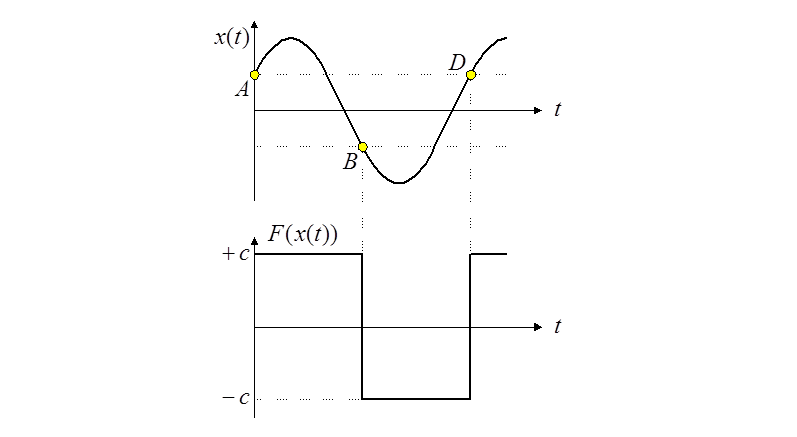
Процесс
разбивается на участки AB, BD
и т.д., где нелинейная функция регулятора принимает значения ![]() или
или ![]() .
.
Уравнение движения на участке AB, его первый и второй интегралы:
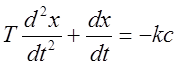 ,
, 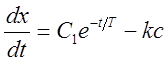 ,
, ![]() .
.
Начальные условия: ![]() ,
, ![]() ,
, ![]() . Откуда
. Откуда ![]() ,
, ![]() .
.
Уравнение движения на участке BD, его первый и второй интегралы (время на каждом участке отсчитывается от нуля):
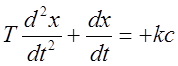 ,
, 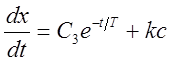 ,
, ![]() .
.
Здесь начальные условия определяются решением на предыдущем участке:
![]() .
.
Постоянные ![]() и
и ![]() известны,
а
известны,
а ![]() определяется из соотношения
определяется из соотношения
![]() .
.
Таким образом,
начальные условия для участка BD имеют вид: ![]() ,
, ![]() ,
, ![]() . Отсюда постоянные интегрирования
. Отсюда постоянные интегрирования ![]() ,
, ![]() .
.
И так далее.
Определим
периодическое решение. В этом случае интервал AD
– период колебаний. Так как полупериоды антисимметричны, достаточно рассмотреть
один полупериод (его длительность ![]() ) – интервал AB.
) – интервал AB.
Сшиваем начало
и конец интервала AB (теперь ![]() – предмет определения):
– предмет определения):
![]() ,
, ![]() .
.
Из первого условия:
![]() , откуда
, откуда 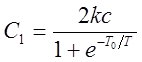 .
.
Второе условие даёт:
![]() ,
, ![]() .
.
Исключая ![]() и
и
![]() , получим:
, получим:
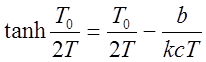 .
.
Здесь одна
неизвестная величина – полупериод ![]() . Трансцендентное
уравнение решается графически. После этого можно вычислить амплитуду колебаний.
. Трансцендентное
уравнение решается графически. После этого можно вычислить амплитуду колебаний.
Метод гармонической линеаризации.
Исследование систем второго порядка даёт наглядное представление о поведении нелинейных систем. Однако большинство систем автоматического регулирования описываются уравнениями более высокого порядка.
Наиболее распространённым методом исследования нелинейных систем выше второго порядка является метод гармонической линеаризации (приближённый метод).
Пусть имеется нелинейное звено с характеристикой
![]() .
.
Подадим на вход этого звена
гармонический сигнал ![]() . На выходе получим
. На выходе получим
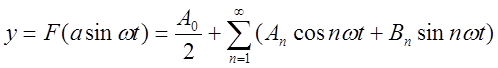 .
.
Допустим, что в замкнутой системе возможны автоколебания. Пусть остальная часть системы является линейной, причём величина амплитудной характеристики на частотах высших гармоник значительно меньше, чем для первой
![]() ,
, ![]() ,
,
т.е. линейная часть системы
обладает свойством фильтра. Тогда на входе нелинейного звена сигнал
будет почти гармоническим:![]() .
.
Сигнал на выходе нелинейного звена определяется либо графически, либо посредством разложения его в ряд Фурье. В итоге, в случае симметричных колебаний, задача сводится к определению частоты и амплитуды первой гармоники колебаний.
Пусть первая гармоника сигнала на выходе нелинейного элемента имеет вид:
![]() .
.
Здесь введены стандартные обозначения. Кроме того, заметив, что
![]() , получим
, получим 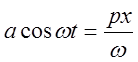 . Здесь
. Здесь
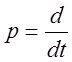 .
.
В результате
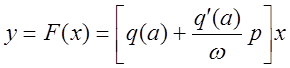 ,
,
где
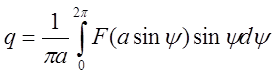 ,
, 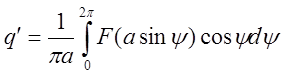 ,
, ![]() .
.
Это
представление называется гармонической линеаризацией нелинейности, а
величины ![]() и
и ![]() – коэффициентами
гармонической линеаризации. Для данного конкретного периодического решения
– коэффициентами
гармонической линеаризации. Для данного конкретного периодического решения ![]() , т.е. связь между x
и y формально линейна. Нелинейность заключена в
зависимости коэффициентов гармонической линеаризации от амплитуды.
, т.е. связь между x
и y формально линейна. Нелинейность заключена в
зависимости коэффициентов гармонической линеаризации от амплитуды.
Амплитудно-фазовая
характеристика нелинейного звена (подстановка ![]() )
)
![]()
зависит только от амплитуды и не зависит от частоты – в противоположность характеристикам линейных звеньев.
Пример. Кубическая нелинейность.
Пусть
![]() .
.
Так как нелинейность
симметричная, то ![]() , а
, а
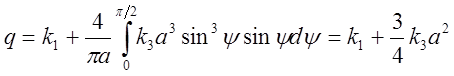 .
.
Пример. Петлевая релейная характеристика.
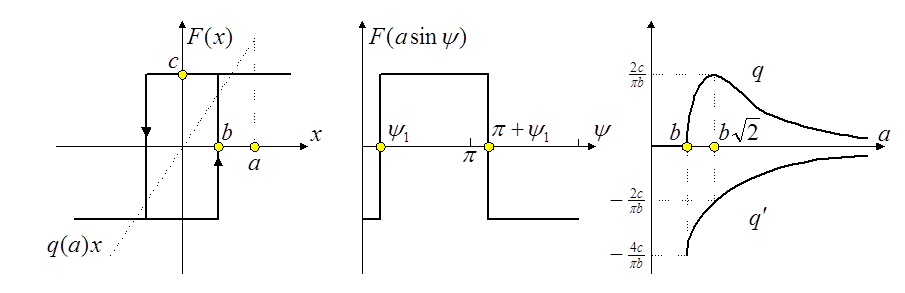
Угол переключения определяется
соотношением ![]() . В результате
. В результате
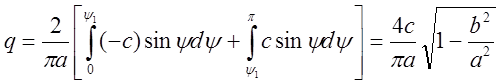 ,
,
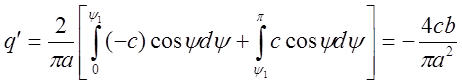 .
.
Соответствующие графики
изображены на рисунке выше (![]() ).
).
Видно, что
гистерезисная петля приводит к запаздыванию (![]() ),
которое уменьшается с ростом амплитуды входного сигнала, так как эффект петли
падает.
),
которое уменьшается с ростом амплитуды входного сигнала, так как эффект петли
падает.
Таким образом, гармоническая линеаризация переводит нелинейное координатное запаздывание в запаздывание по фазе, характерное для линейных систем, но с существенным отличием – зависимостью фазового сдвига от амплитуды входного сигнала, чего нет в линейных системах.
Пример. Однозначные релейные характеристики.
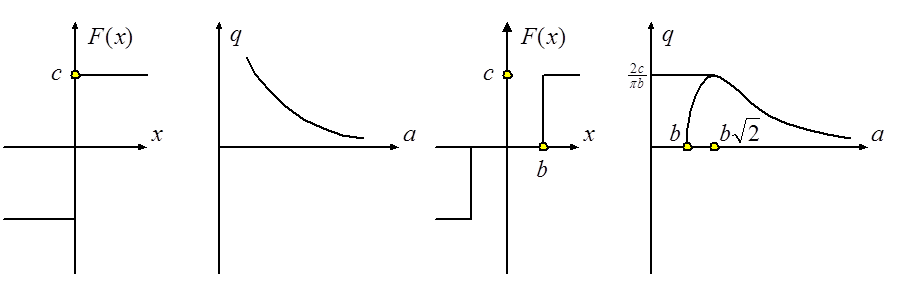
Здесь
![]() ,
, 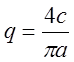 ,
, 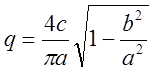 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.