Критерии устойчивости линейной системы. Критерий устойчивости Рауса-Гурвица

Критерии устойчивости линейной системы [1].

          Устойчивость системы управления – способность возвращаться в состояние равновесия после исчезновения внешних сил.

          Если с течением времени изображающая точка в фазовом пространстве координат системы стремится к началу координат, то система асимптотически устойчива.

          Заметим, что понятие устойчивости можно распространить и на случай движения системы и говорить о невозмущённом движении. Заданное невозмущённое движение будет устойчивым, если после исчезновения возмущения возмущённое движение по истечении некоторого времени войдёт в заданную область: , .

          Дифференциальное уравнение движения системы автоматического регулирования

.

Здесь  – оператор дифференцирования,  – регулируемая величина,  – управляющее воздействие (или возмущение, поскольку характер переходных процессов определяется видом левой части уравнения движения).

Решение этого уравнения есть сумма двух решений – частного решения неоднородного уравнения (с правой частью) – вынужденное решение, и общего решения уравнения (без правой части) – свободное решение (в теории авторегулирования – переходная составляющая):

.

          Система устойчива, если с течением времени переходная составляющая будет стремиться к нулю. Таким образом, необходимо решить уравнение без правой части:

.

Решение ищется в виде

.

Подстановка даёт характеристическое уравнение (множитель  сокращается)

.

Корни этого уравнения определяют переходной процесс:

.

Постоянные интегрирования определяются также видом правой части уравнения движения, поэтому форма переходного процесса определяется как левой, так и правой частями исходного уравнения. Тем не менее, устойчивость линейной системы определяется только характеристическим уравнением.

Очевидно, что для затухания переходного процесса необходимо и достаточно, чтобы вещественные части всех корней характеристического уравнения были отрицательными – лежали слева от мнимой оси плоскости корней.

Плоскость корней:

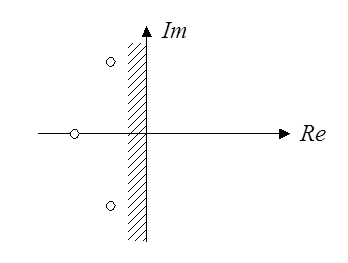
Система будет находиться на границе устойчивости при наличии

          1. Нулевого корня,

          2. Пары чисто мнимых корней.

В первом случае . Это значит, что в характеристическом уравнении отсутствует свободный член: . В этом случае дифференциальное уравнение движения будет иметь вид

,

и система будет устойчивой не относительно регулируемой величины , а относительно скорости её изменения . Такая система называется нейтрально устойчивой.

          Во втором случае система будет иметь незатухающие гармонические колебания с постоянной амплитудой.

          Можно судить об устойчивости системы, не решая характеристического уравнения.

          Так, необходимым (но не достаточным) условием устойчивости системы является положительность всех коэффициентов характеристического уравнения.

          Доказательство.

          Коль скоро система устойчива, то все корни имеют отрицательные действительные части. Запишем характеристическое уравнение в виде

.

Скобки с чисто действительными корнями будут иметь вид .

Пара скобок с комплексными корнями будет иметь вид

.

Коль скоро в тех и других скобках нет компонентов со знаком «минус», неоткуда появиться знаку «минус» при раскрытии всех скобок.

Критерий устойчивости Рауса-Гурвица [1].

Задача об отыскании критерия устойчивости для систем, описываемых дифференциальными уравнениями любого порядка, была сформулирована Максвеллом в 1868 году и решена Раусом в 1877 году в форме алгоритма – последовательности математических операций.

В 1895 году Гурвиц сформулировал критерий в алгебраической форме.

Составляется квадратная матрица

.

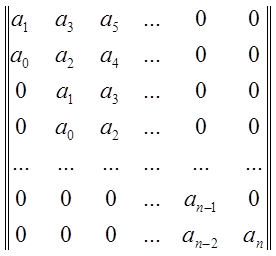При  должны быть больше нуля следующие определители:

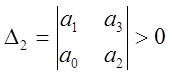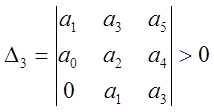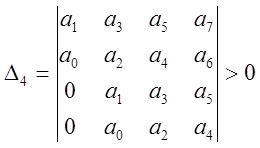, , ,  и т.д.

Последний определитель включает в себя всю матрицу. Он выражается через предпоследний определитель:

, что сводится к требованию , так как .

Система будет на границе устойчивости при  и  ().

Это возможно либо при , либо при . При  имеет место апериодическая устойчивость, при  – колебательная.

Уравнение первого порядка:

.

Критерий Гурвица:

.

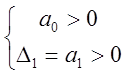Уравнение второго порядка:

.

Критерий Гурвица:

.

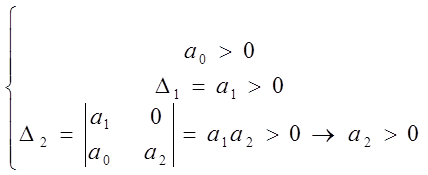Уравнение третьего порядка:

.

Критерий Гурвица:

.

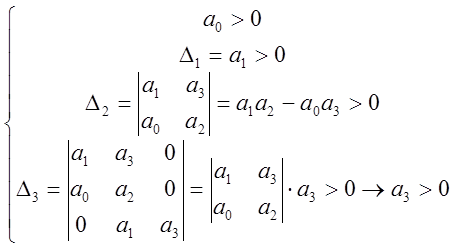 – уже недостаточно положительности коэффициентов характеристического уравнения.

Уравнение четвёртого порядка:

.

Определитель Гурвица:

.

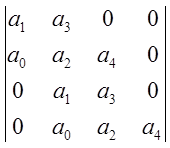Кроме положительности коэффициентов, требуется выполнение условия

.

Уравнение пятой степени:

.

Определитель Гурвица:

.

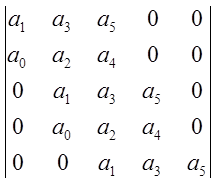Кроме положительности коэффициентов, требуется выполнение двух условий:

.

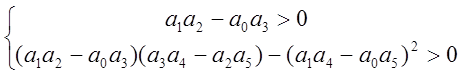Использование этого критерия практически ограничивается уравнениями четвёртого порядка.

Критерий устойчивости Михайлова [1].

Характеристический полином (знаменатель передаточной функции):

.

Характеристический комплекс:

.

Вещественная часть содержит только чётные степени :

,

а мнимая – только нечётные:

.

Критерий Михайлова (1936):