Критерии устойчивости линейной системы. Критерий устойчивости Рауса-Гурвица, страница 2

Характеристический полином не будет иметь корней в правой полуплоскости, если полное приращение фазы  при изменении  от нуля до бесконечности будет равно , где n – степень характеристического полинома D(p).

Доказательство.

Характеристический комплекс  – точка на комплексной плоскости (X,Y). При изменении частоты описывается кривая – годограф Михайлова. Определим угол её поворота.

Запишем характеристический вектор в виде:

 

 – произведение n комплексных чисел.

При перемножении аргументы комплексных чисел складываются, поэтому результирующий угол поворота вектора  при изменении  от нуля до бесконечности будет равен сумме углов поворота отдельных сомножителей.

          Пусть, например, корень  – вещественный и отрицательный, т.е. . Вид соответствующего сомножителя

.

Годограф представляет собой вертикальную линию, исходящую из точки А на оси Х, уходящую в бесконечность.

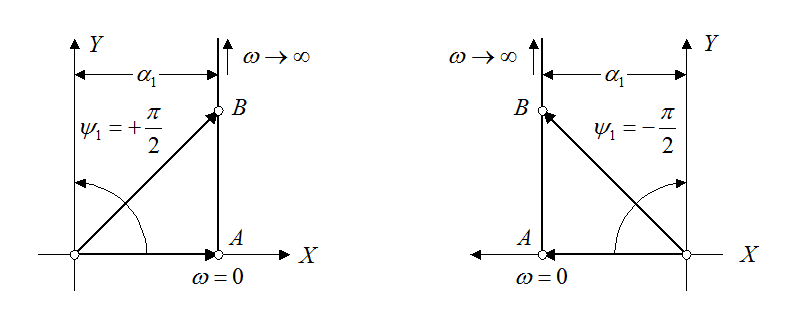
Результирующий угол поворота вектора 0В . При  (справа на рисунке) соответствующий угол поворота .

Пусть два корня, например, корни  и , комплексно сопряжённые с отрицательной вещественной частью, т.е. . Вид соответствующих сомножителей:

.

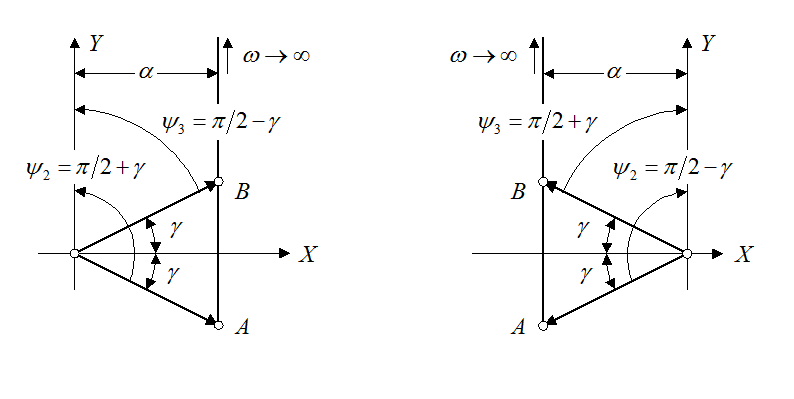
Здесь угол .

Годографы представляют собой вертикальные линии, исходящие из точек А и В, уходящие в бесконечность.

Результирующие углы поворота векторов 0А и 0В, соответственно,  и . Вектор, соответствующий произведению , повернётся на угол . При  (справа на рисунке) соответствующий угол поворота .

          Таким образом, если характеристическое уравнение будет иметь l корней с положительной вещественной частью, то, каковы бы ни были эти корни (вещественные или комплексные), сумма углов поворотов будет равна . Все остальные  корней дадут сумму углов поворотов . В результате общий угол поворота вектора  будет равен:

.

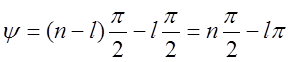          Для устойчивости системы необходимо и достаточно, чтобы .

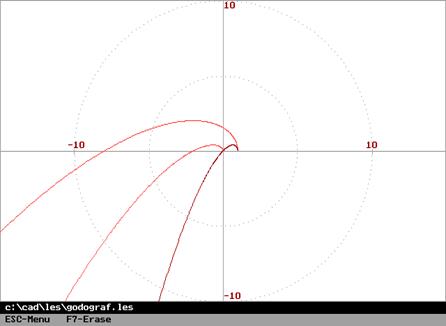
Годограф Михайлова всегда имеет форму плавной спирали, конец которой уходит в бесконечность в том квадранте комплексной плоскости, номер которого равен степени характеристического полинома. Годографы на рисунке ниже слева соответствуют полиномам

,

,

,

,

,

.

 

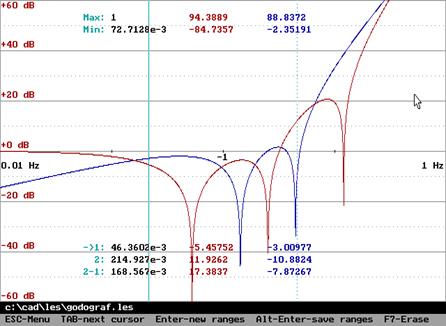
Неустойчивость системы всегда связана с тем, что нарушается последовательность прохождения квадрантов годографом Михайлова, и угол поворота оказывается меньше, чем .

          Критерий Михайлова может быть сформулирован иначе.

          Для устойчивости системы годограф Михайлова проходит последовательно n квадрантов. Поэтому корни уравнений  и  должны чередоваться (на рисунке выше справа , ).

          Границы устойчивости первого и второго типа (нулевой корень и колебательная граница устойчивости).

Нулевой корень – отсутствует свободный член () и кривая идёт из начала координат.

Колебательная граница устойчивости

 

 – точка  попадает в начало координат (при этом  – частота незатухающих колебаний).

Построение области устойчивости. D-разбиение.

          Значения тех или иных параметров системы могут влиять на её устойчивость. В этом случае определяют области устойчивости. Ограничимся двумя параметрами.

          Пусть характеристическое уравнение имеет вид (откуда оно берётся, рассмотрим позже):

.

Критерий устойчивости Рауса-Гурвица (удобен для систем не выше четвёртого порядка):

.

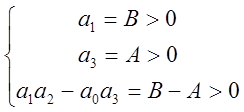Формально граница устойчивости первого типа (нулевой корень) определяется равенством . Граница устойчивости колебательного типа определяется равенством .

Для уравнений любого порядка удобен критерий Михайлова. Колебательной границе устойчивости соответствует равенство , которое распадается на два уравнения

.

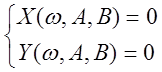Эта система уравнений параметрически описывает границу области устойчивости (здесь параметром является  – частота гармонических колебаний системы) – при соблюдении дополнительного условия отрицательности вещественных частей всех остальных корней, кроме чисто мнимых.

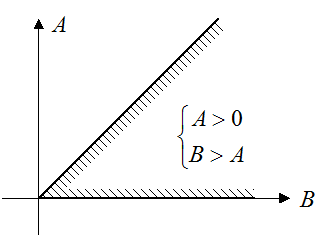
Совокупность всех кривых на плоскости параметров называется D-разбиением. Из всего комплекса этих кривых собственно границы области устойчивости определяются по следующему правилу.

Перемещаясь вдоль кривой в сторону увеличения , надо штриховать её с левой (правой) стороны, если будет положительным (отрицательным) определитель

.

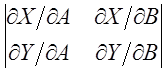Штриховка будет направлена внутрь области устойчивости, если параметр А отложен по оси абцисс вправо, а параметр В – по оси ординат вверх.

Пример – дистанционная следящая система.

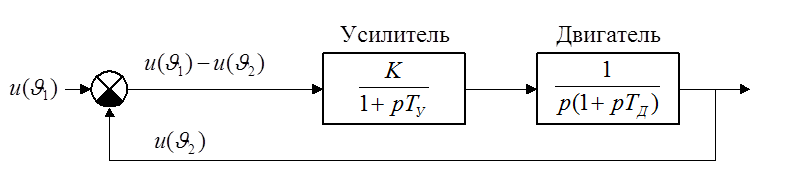
Здесь  – углы поворотов командной и исполнительной осей,  – постоянная времени усилителя и электромеханическая постоянная времени двигателя (заданная величина). Требуется построить область устойчивости в плоскости двух параметров – общего коэффициента усиления К и постоянной времени усилителя.

Передаточная функция разомкнутой цепи:

.

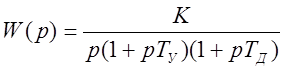Характеристическое уравнение:

, .

Характеристический комплекс:

.

Уравнения, определяющие границу области устойчивости:

.

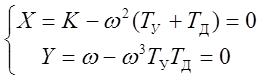Решение:

, .

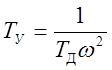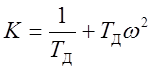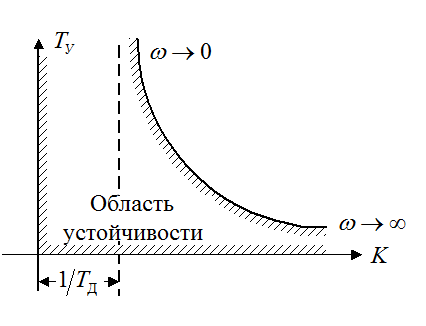
Знак определителя:

, , , .

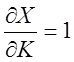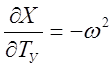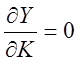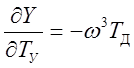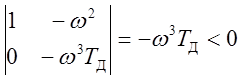
 – штриховка справа.