YI семестр. ММФ НГУ
Методы вычислений. МКЭ
КОНСПЕКТ СЕМИНАРСКИХ ЗАНЯТИЙ
Мацокин А.М. – проф. кафедры вычислительной математики
2005-2006 учебный год
Предлагаем Вашему вниманию конспект семинарских занятий по второй половине курса «Методы вычислений» (лектор проф. Ю.М. Лаевский), проведенных профессором кафедры А.М. Мацокиным.
Содержание
1 семинар "Метод Галеркина (Ритца, Бубнова) для решения задачи о представлении линейного функционала в гильбертовом пространстве". - 2 -
Гильбертово пространство. - 2 -
Линейный функционал. - 2 -
Теорема Рисса. - 2 -
Эквивалентные нормировки. - 2 -
Задача о представлении линейного функционала. - 3 -
· Проекционная формулировка: - 3 -
· Вариационная формулировка: - 3 -
Решение (приближенное): - 3 -
Сходимость. - 3 -
2 семинар "Пример построения проекционной формулировки краевой задачи и выбора конечномерных подпространств в методе Галеркина". - 5 -
Краевая задача: - 5 -
Интегральное тождество. - 5 -
Энергетическое пространство. - 5 -
Проекционная формулировка задачи : - 6 -
Тригонометрический
базис в 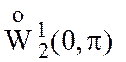 . - 6 -
. - 6 -
Метод
Галеркина для задачи в ![]() . - 7 -
. - 7 -
3 семинар "Кусочно-линейные восполнения". - 8 -
Метод
Галеркина для задачи в ![]() . - 10 -
. - 10 -
4 семинар "Кусочно-квадратичные восполнения". - 11 -
Метод
Галеркина для задачи в ![]() . - 13 -
. - 13 -
Задачи к экзамену. - 15 -
Пространство (бесконечномерное) ![]() – гильбертово, если в нем заданы:
– гильбертово, если в нем заданы:
·
скалярное произведение ![]() ,
,
·
норма ![]() ;
;
оно замкнуто и сепарабельно.
·
В нем существует счетный базис ![]() и
и 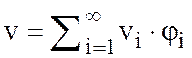 .
.
·
Среди всех базисов выделяют ортонормированные базисы: ![]()
![]()
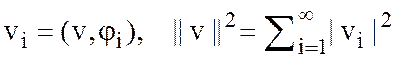 .
.
·
Если ![]() – замкнутое подпространство, то
элементы, ортогональные ко всем элементам из
– замкнутое подпространство, то
элементы, ортогональные ко всем элементам из ![]() ,
образуют замкнутое ортогональное подпространство
,
образуют замкнутое ортогональное подпространство ![]() и
и ![]() , т.е.
, т.е.
![]() .
.
Отображение ![]() называется линейным
функционалом, если
называется линейным
функционалом, если
1. ![]() – однородность,
– однородность,
2. ![]() – аддитивность,
– аддитивность,
3. ![]() – ограниченность (непрерывность).
– ограниченность (непрерывность).
Линейный функционал f(v) однозначно представим в виде ![]() .
.
Пусть ![]() – билинейная,
симметричная форма, определенная на плотном в
– билинейная,
симметричная форма, определенная на плотном в ![]() множестве
множестве ![]() :
:
·
![]()
– линейность по первому аргументу,
·
![]() – симметричность,
– симметричность,
Кроме того,
·
![]() – непрерывность формы,
– непрерывность формы,
·
![]() – коэрцитивность формы.
– коэрцитивность формы.
Доказать, что форма ![]() продолжается по непрерывности на
продолжается по непрерывности на ![]() с сохранением всех своих свойств,
определяет в H новое скалярное
произведение и норму
с сохранением всех своих свойств,
определяет в H новое скалярное
произведение и норму ![]() , эквивалентную норме
, эквивалентную норме ![]() :
:
![]() .
.
определить ![]() .
.
определить 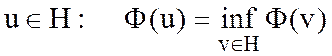 , где
, где ![]() .
.
Выберем (произвольно) в гильбертовом пространстве ![]() несколько линейно независимых элементов:
несколько линейно независимых элементов: ![]() .
.
Их линейную оболочку обозначим через ![]() .
.
Будем искать приближенное решение в виде ![]() .
.
Для определения неизвестных ![]() чисел
чисел ![]() из проекционных условий
из проекционных условий
![]()
получим n уравнений:
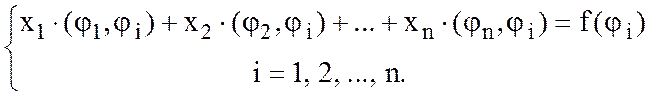
Для определения неизвестных ![]() чисел
чисел ![]() из вариационных условий
из вариационных условий
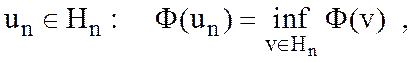
где ![]() , приравняем нулю
производные от функционала
, приравняем нулю
производные от функционала 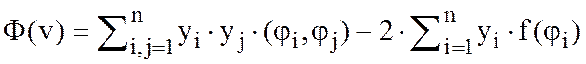 :
:
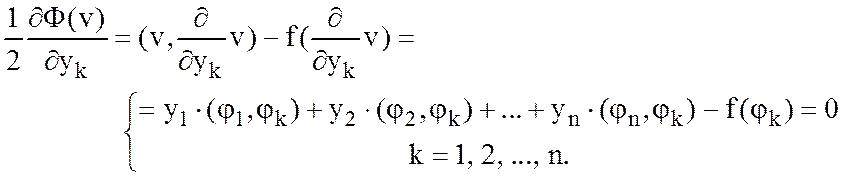
Легко видеть, что обе
формулировки приводят к одной и той же системе линейных алгебраических
уравнений порядка ![]() с матрицей
Грамма набора линейно независимых векторов
с матрицей
Грамма набора линейно независимых векторов ![]() .
.
Доказать,
что эта матрица является невырожденной, симметричной и положительно определенной, т.е. система имеет единственное решение.
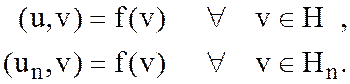
![]()
Отсюда следует, что приближенное решение совпадает с
ортогональной проекцией решения на ![]() .
.
Для сходимости достаточно, чтобы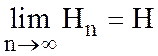 , т.е.
, т.е.
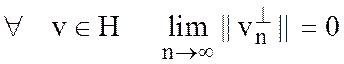 .
.
Обычно для оценки сходимости используют следующее из теоремы Пифагора неравенство:
![]() ,
,
подбирая для (неизвестного) ![]() подходящий
элемент (интерполянт)
подходящий
элемент (интерполянт) ![]() и оценивая их разность.
и оценивая их разность.
Задача 1.
![]() ,
, ![]() ,
, ![]()
а. определить
![]() ;
;
б. определить 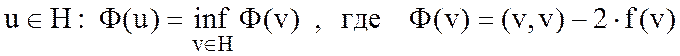 .
.
Задача 2.
![]() ,
, ![]() ,
, ![]()
а. определить
![]() ;
;
б. определить 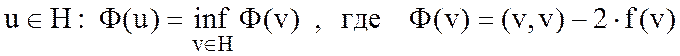 .
.
Задача 3.
![]() ,
, 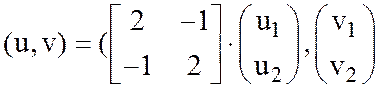 ,
, ![]()
а. определить
![]() ;
;
б. определить 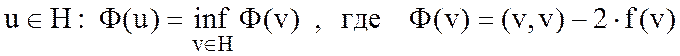 .
.
Задача 4.
![]() ,
, 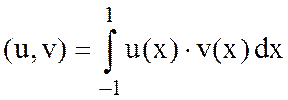 ,
, 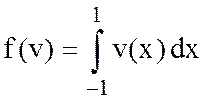
а. определить
![]() ;
;
б. определить 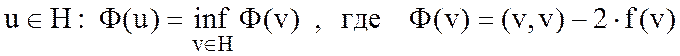 .
.
Задача 5.
![]() ,
, 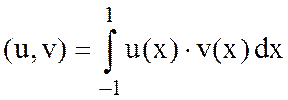 ,
, 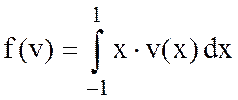
а. определить
![]() ;
;
б. определить 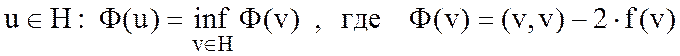 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.