|
|
|
|
вычисление правых частей |
|
|
– |
– |
|
решение систем |
|
|
с диагональной матрицей – |
с 3-диагональной матрицей – |
|
вычисление
приближенного решения в точке |
|
|
– |
– |
из таблицы следует, что кусочно-линейные функции «экономичнее» тригонометрического базиса при одной и той же оценке точности приближения (почему точность одинаковая?).
На сетке ![]() определим дополнительные узлы
определим дополнительные узлы ![]() и по значениям
и по значениям ![]() и
и ![]() построим непрерывное, кусочно-квадратичное
приближение
построим непрерывное, кусочно-квадратичное
приближение ![]() функции
функции ![]() :
:
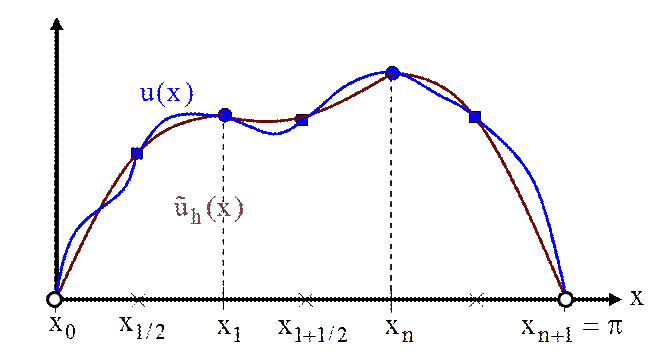
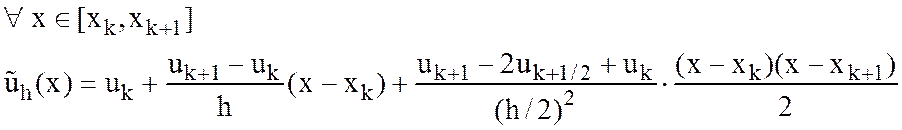
Проверьте, что – интерполяционный полином в форме Ньютона.
Постройте интерполяционный полином ![]() в форме Лагранжа.
в форме Лагранжа.
Ответ:
![]()
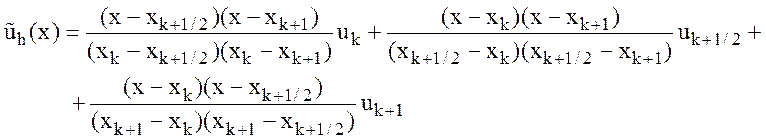
Обозначим через 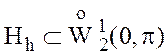 подпространство непрерывных, квадратичных
на каждом интервале
подпространство непрерывных, квадратичных
на каждом интервале ![]() сетки
сетки ![]() функций,
равных нулю в концах интервала
функций,
равных нулю в концах интервала ![]() , и назовем его подпространством
кусочно-квадратичных восполнений.
, и назовем его подпространством
кусочно-квадратичных восполнений.
Определить размерность и построить базис в ![]() .
.
Ответ: размерность равна ![]() (количество
произвольных параметров
(количество
произвольных параметров ![]() , определяющих
восполнение);
, определяющих
восполнение);
самый простой базис соответствует
классическому базису ![]() , с базисными функциями:
, с базисными функциями:
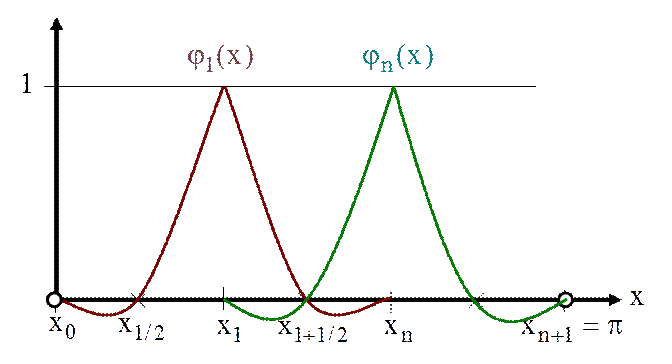
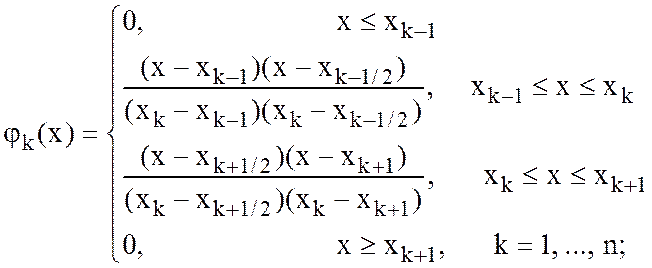
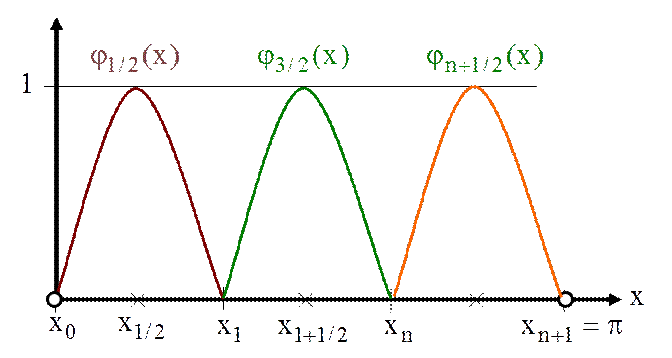
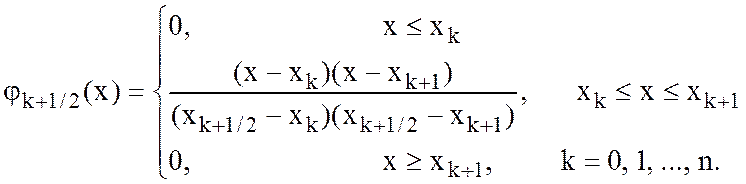
Найти 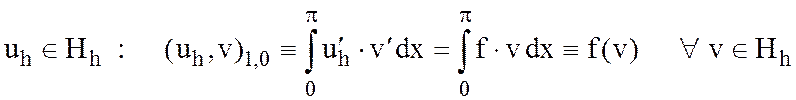 .
.
Построить систему уравнений для определения коэффициентов разложения
![]()
и предложить метод ее решения.
Ответ: система с 5-и диагональной матрицей имеет вид
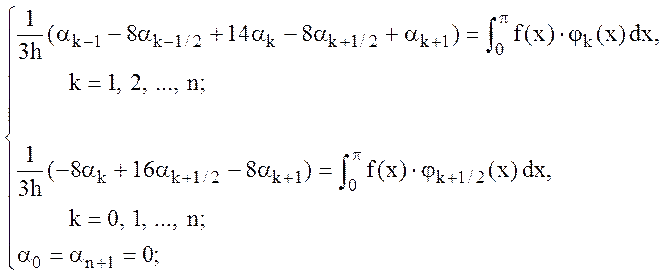
и для ее решения применим метод прогонки для 5-и диагональной матрицы (докажите).
Указание:
сначала проверьте, что система имеет вид:
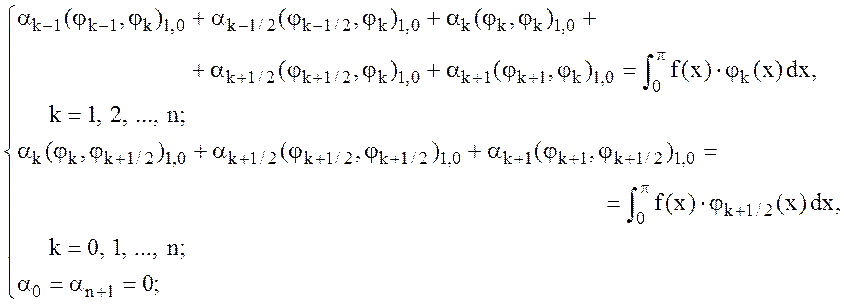
затем вычислите ее коэффициенты:
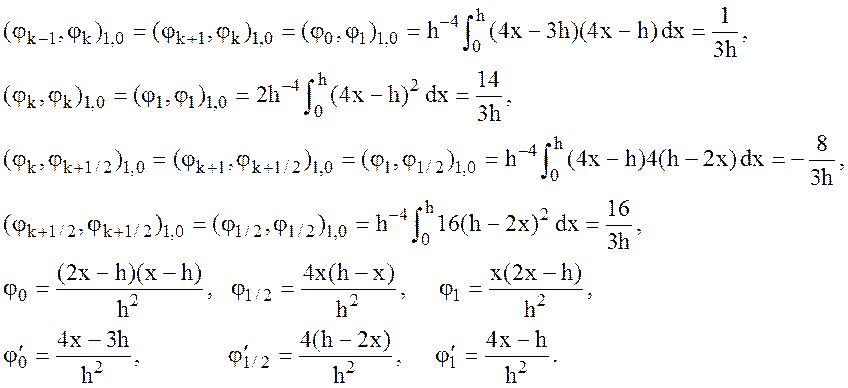
Задача. Доказать оценку
![]()
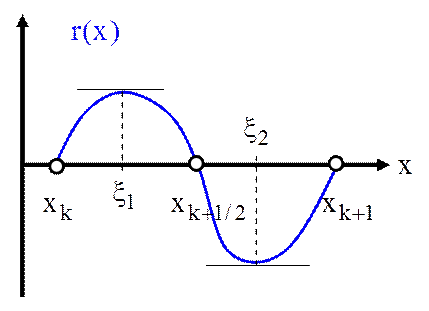
Решение. Сначала заметим, что ошибка ![]() имеет
на интервале
имеет
на интервале ![]() по крайней мере 3 разных корня,
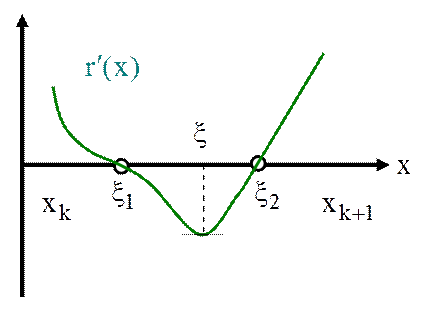
ее первая производная – 2 разных корня
по крайней мере 3 разных корня,
ее первая производная – 2 разных корня ![]() и
и ![]() , ее вторая производная – хотя бы 1 корень
, ее вторая производная – хотя бы 1 корень ![]() .
.
Следовательно,
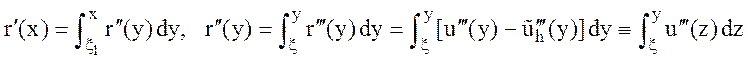
Используя неравенство Коши, получим оценки
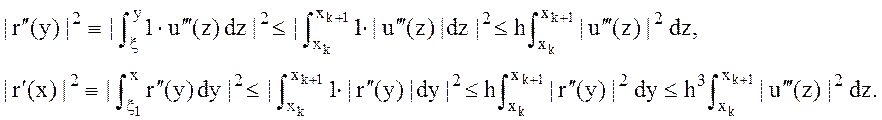
Интегрируя левую и правую
части последней оценки по интервалу ![]() , получим
, получим
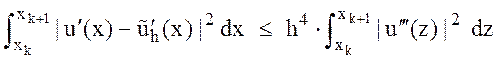 .
.
Суммируя полученное неравенство по всем интервалам, получим
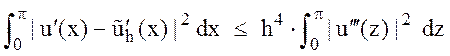 ,
,
т.е. оценку .
Задача. Примените оценку для доказательства неравенства
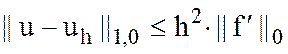 ,
,
где ![]() – приближение по методу
Галеркина с использованием кусочно-квадратичных восполнений решения краевой
задачи с гладкой правой частью:
– приближение по методу
Галеркина с использованием кусочно-квадратичных восполнений решения краевой
задачи с гладкой правой частью:
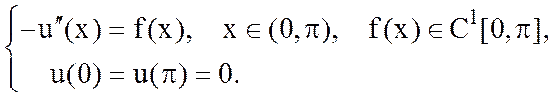
1. Поставить задачу о поиске обобщенного решения для краевой задачи
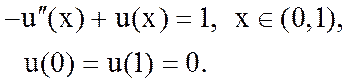
2. Поставить задачу о поиске обобщенного решения для краевой задачи
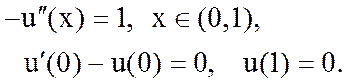
3. Поставить задачу о поиске обобщенного решения для краевой задачи
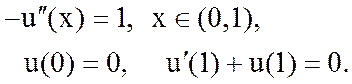
4. Поставить задачу о поиске обобщенного решения для краевой задачи
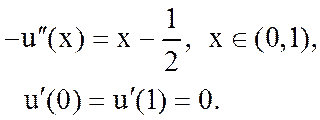
5. Поставить задачу о поиске обобщенного решения для краевой задачи
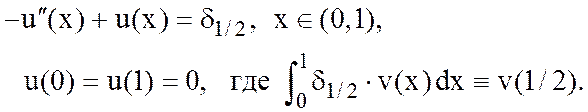
6. Обосновать применимость метода Ритца для задачи о минимуме функционала
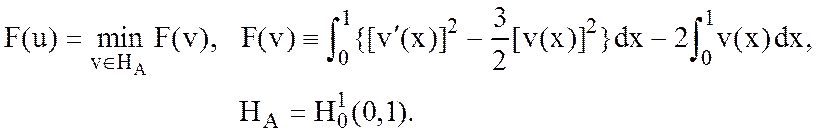
7. Обосновать применимость метода Ритца для задачи о минимуме функционала
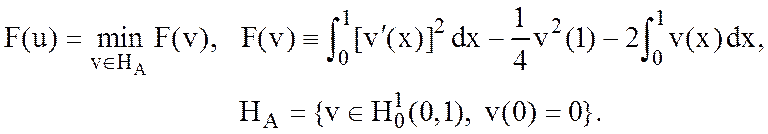
8. Обосновать применимость метода Ритца для задачи о минимуме функционала
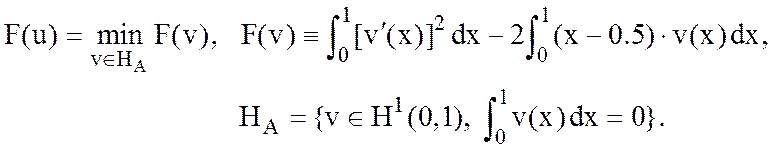
9. Для краевой задачи
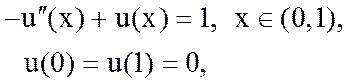
построить схему МКЭ для поузлового базиса на сетке
![]()
10. Для краевой задачи
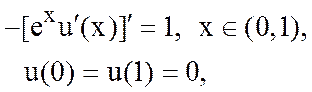
построить схему МКЭ для поузлового базиса на сетке
![]()
11. Для краевой задачи
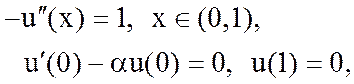
построить схему МКЭ для поузлового базиса на сетке
![]()
12. Для краевой задачи
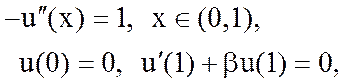
построить схему МКЭ для поузлового базиса на сетке
![]()
$ А.Н. Колмогоров, С.В. Фомин. "Элементы теории функций и функционального анализа", М., изд-во "Наука", 1972 г.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.