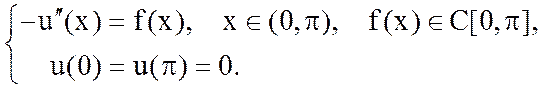
Очевидно, что решение задачи ![]() .
.
Пусть
![]()
– линейное множество плотное в ![]() со
скалярным произведением
со
скалярным произведением
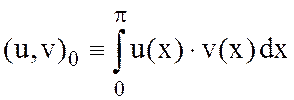
Доказать, что решение задачи удовлетворяет тождеству
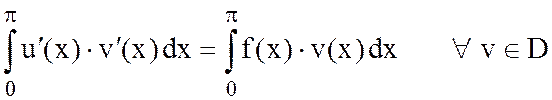 .
.
Доказать,
что билинейная форма 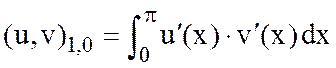 определяет на
множестве функций
определяет на
множестве функций ![]() скалярное произведение
и норму
скалярное произведение
и норму 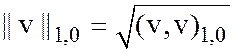 .
.
Пополним ![]() по норме
по норме 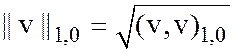 , в результате получим гильбертово
пространство
, в результате получим гильбертово
пространство 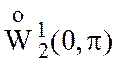 .
.
Доказать, что 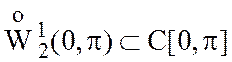 , т.е.
, т.е.
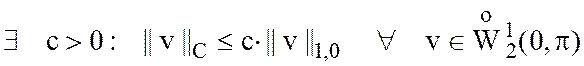 .
.
Доказать, что ![]() функционал
функционал
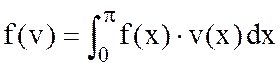 – линейный и непрерывный в
– линейный и непрерывный в 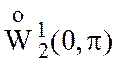 .
.
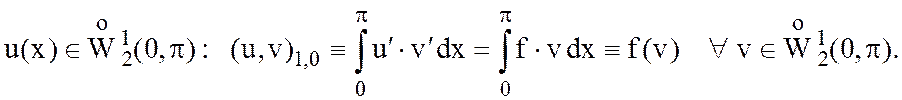
Доказать: решение задачи совпадает с решением задачи .
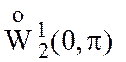 .
.Известно$, что в ![]() системы
функций
системы
функций
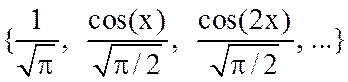 и
и 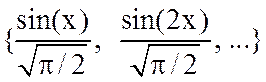
образуют ортонормированные базисы, т.е. ![]() :
:
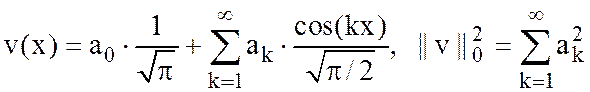 ,
,
где 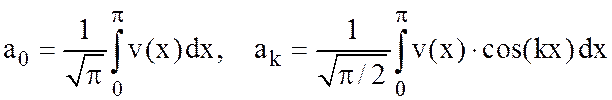 ;
;
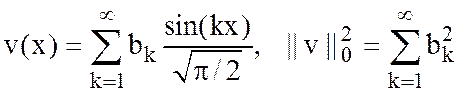 ,
,
где 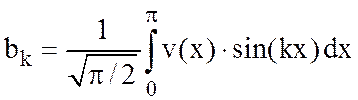 .
.
Доказать, что 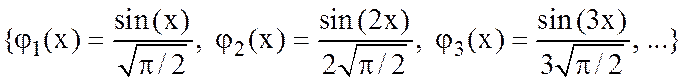
– ортонормированный базис в 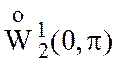 со скалярным произведением
со скалярным произведением 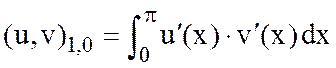 .
.
Доказательство.
1)
Очевидно, что 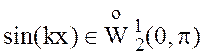 и легко проверить, что
и легко проверить, что
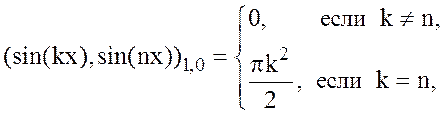
т.е.
система функций 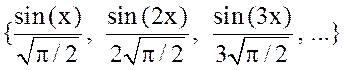 ортонормальна в
ортонормальна в 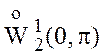 .
.
2)
Просуммируем проекции функции 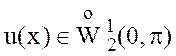 на
на ![]() :
:
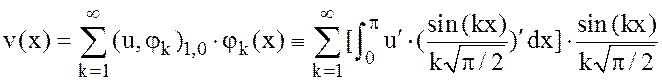
и
нам нужно доказать, что ![]() .
.
3)
Так как ![]() и
и 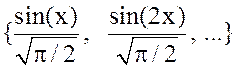 –
ортонормированный базис в
–
ортонормированный базис в ![]() , то
, то
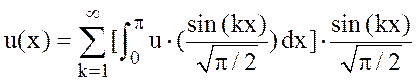
и так как
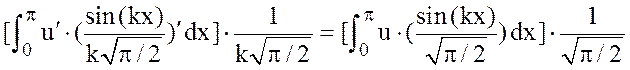
(проверьте это равенство), то ряды и .
Доказать:
если 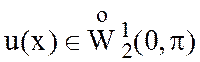 и
и ![]() , то для ее проекции на
, то для ее проекции на 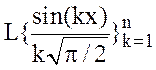 :
:
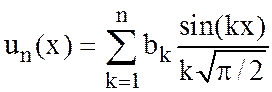 , где
, где 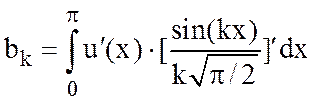
справедлива оценка
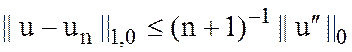
Доказательство.
Из и разложения ![]() в ряд имеем
в ряд имеем
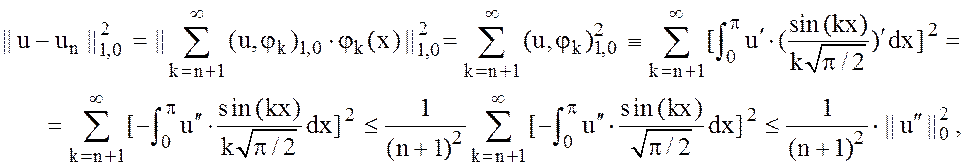
что и требовалось доказать.
Найти ![]() .
.
Построить систему уравнений для определения коэффициентов разложения
![]() .
.
Ответ:  .
.
Доказать: 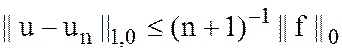 (следствие
).
(следствие
).
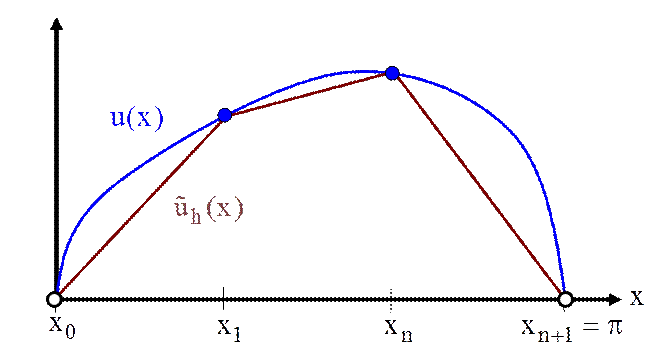
Построим на интервале ![]() сетку
сетку ![]() и по
значениям
и по
значениям ![]() построим непрерывное, кусочно-линейное
приближение
построим непрерывное, кусочно-линейное
приближение ![]() функции
функции ![]() :
:
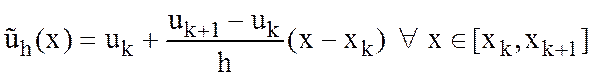
Доказать оценки:
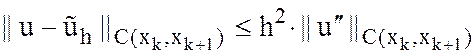 ,
,
![]() .
.
Доказательство.
Для
доказательства используем разложения в ряд Тейлора в точке ![]() :
:
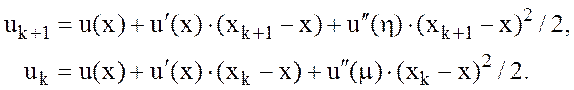
Тогда
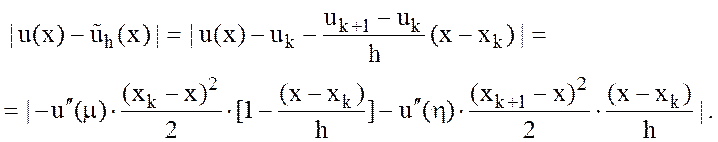
Так
как ![]() и
и ![]() , то
, то
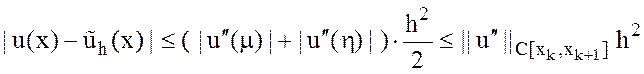 ,
,
т.е. получили оценку .
Аналогично получим оценку :
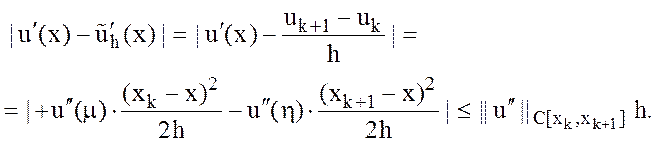
Доказать оценку:
![]() .
.
Доказательство.
Оценим квадрат ошибки приближения, используя элементарные тождества и неравенство Коши:
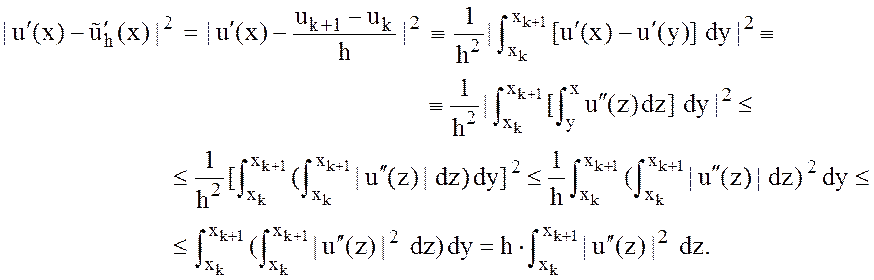
Интегрируя
левую и правую части этой оценки по интервалу ![]() ,
получим
,
получим
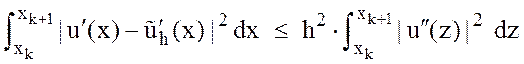 .
.
Суммируя полученное неравенство по всем интервалам, получим
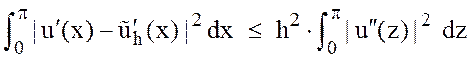 ,
,
т.е. оценку .
Обозначим через 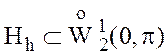 подпространство непрерывных, линейных на
каждом интервале
подпространство непрерывных, линейных на
каждом интервале ![]() сетки
сетки ![]() функций,
равных нулю в концах интервала
функций,
равных нулю в концах интервала ![]() , и назовем его подпространством
кусочно-линейных восполнений.
, и назовем его подпространством
кусочно-линейных восполнений.
Определить размерность и построить базис в ![]() .
.
Ответ: размерность равна ![]() (количество
произвольных параметров
(количество
произвольных параметров ![]() , определяющих
восполнение);
, определяющих
восполнение);
самый простой базис соответствует
классическому базису ![]() , с базисными функциями (
, с базисными функциями (![]() ):
):
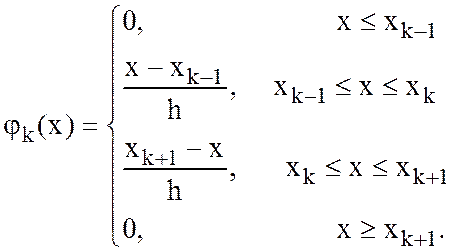
Найти ![]() .
.
Доказать:![]() (следствие
оценки ).
(следствие
оценки ).
Построить систему уравнений для определения коэффициентов разложения
![]()
и предложить метод ее решения.
Ответ: система с трехдиагональной матрицей имеет вид
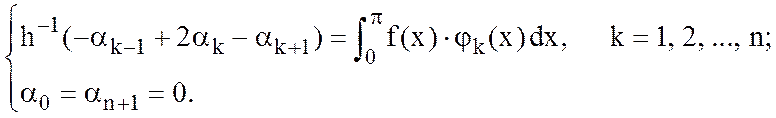 .
.
и для ее решения применим метод прогонки (докажите).
Оцените объем вычислений приближенного решения задачи в подпространстве с тригонометрическим базисом и в подпространстве кусочно-линейных восполнений.
Ответ (будем считать, что при
вычислении интегралов ![]() заменяется непрерывным, кусочно-линейным
интерполянтом
заменяется непрерывным, кусочно-линейным
интерполянтом ![]() ):
):
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.