Динамика твердого тела. Изменение момента импульса равняется моменту силы

Лекция 7.

Динамика твердого тела.

Момент сил относительно неподвижной точки.

            Ранее был определен момент импульса частицы относительно некоторого начала отсчета. По аналогии введем момент силы относительно заданного начала отсчета. Для простоты будем считать начало отсчета покоящимся. Итак:

                                                  (1)

- векторное произведение радиус вектора направленного в мгновенное положение частицы на силу , действующую на частицу (см рис. n1). Физический смысл, результат и направление результата -очевиден: вектор направлен перпендикулярно одновременно и и , т.е перпендикулярен плоскости в которой лежат  ,. Модуль вычисляется по правилу:

.

Если на частицу действует не единственная сила -, то, очевидно, полный момент складывается из моментов, создаваемых всеми силами:

                        (2)

Основное уравнение динамики твердого тела. Уравнение моментов.

            Допустим, что т. O – начало отсчета неподвижна. Найдем скорость изменения момента импульса частицы относительно заданной т. О.

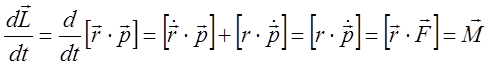                         (3)

Изменение момента импульса равняется моменту силы. Это есть основное уравнение динамики твердого тела. Сравните с формулировкой II-го закона Ньютона: изменение импульса равно действующей силе.

Уравнение моментов системы материальных точек.

            Пусть имеется система материальных точек, пронумерованных от  до . На каждую -ю материальную точку действуют силы со стороны остальных и внешняя сила . Моменты этих сил обозначим соответственно:  , . Выпишем уравнения моментов для каждой частицы:

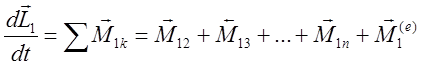
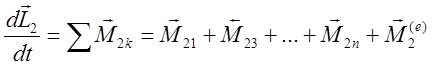                      (4)

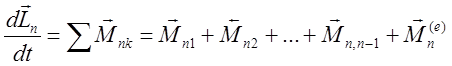
Складывая почленно левые и правые части (4) убеждаемся, что :

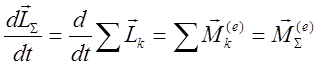                              (5)

Изменение полного момента импульса всей системы материальных точек равно сумме моментов внешних! сил . Последнее утверждение следует из того, что для любой пары , поскольку в силу III – го закона Ньютона . Любое «твердое» тело можно представить семейством материальных точек с неизменными взаимными расстояниями между ними и равными и противоположно направленными взаимными силами.

Закон сохранения момента импульса твердого тела.

Допустим, что твердое тело моделируется набором материальных точек. Тогда, если , то согласно (5) 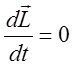, или . Изменение момента импульса равно нулю. Момент импульса сохраняется если сумма моментов внешних сил равна нулю. – фундаментальный закон сохранения момента импульса.

Это утверждение было доказано, в частности, для полей центральных сил. В поле центральных сил, по – определению, момент сил действующих на частицу равен нулю, т.к. сила и радиус - вектор частицы антипараллельны.

Преобразование момента импульса и момента сил при смещении начала отсчета системы координат.

Рассмотрим момент импульса произвольной частицы, находящейся в некоторой т. P относительно систем отсчета, центрированных в т.  см. рис. n2. Радиус векторы частицы относительно этих начал соответственно . Обозначим , где . Подставим соотношение между радиус векторами в выражение для момента импульса:

                     (6)

Аналогично:

                                                       (7)

Для множества материальных точек суммирование по всем точкам дает:

Если полный импульс системы , то  - момент импульса системы не зависит от выбора начала отсчета.

Для системы частиц, следуя (7), нетрудно убедиться, что . Если результирующая сила равна нулю, как в случае действующей пары сил, то  . В этом случае момент сил не зависит от выбора начала отсчета.

Момент импульса и момент сил относительно неподвижной оси.

Векторное уравнение (3) в декартовых координатах эквивалентно 3-м уравнениям:

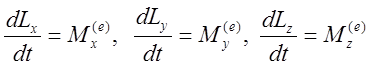                                 (8)

Допустим, что система частиц способна вращаться относительно единственной оси, например оси , так, что существующие моменты сил будут приводить лишь к деформации оси и возникновению ответных моментов сил в «подшипниках» на которые опирается ось вращения. Для простоты положим  . В таком случае уравнения (8) упрощаются . Для расчета момента внешних сил удобно ввести компоненты радиус - вектора частицы и действующей силы в направлении поперечном и продольном относительно оси. Обозначим . Используя эти разложения можно убедиться, что . Последнее слагаемое в сумме равно нулю как векторное произведение параллельных векторов. Слагаемые в скобках направлены перпендикулярно выбранной оси, следовательно их компоненты в направлении выбранной оси также равны нулю. Окончательно