Динамика твердого тела. Изменение момента импульса равняется моменту силы, страница 4

Теорема Эйлера.

В плоском движении твердое тело может быть переведено из любого положения в другое произвольное путем одного поворота вокруг некоторой оси. (частный случай теоремы Л.Эйлера). Доказательство. Выделяется пара точек  на плоскости, в которой происходит движение твердого тела. Рассматривается сдвиг прямой  в новое положение . Соединяя с, с и, проводя перпендикуляры из середин ,   до пересечения в т.  находим мгновенную ось вращения. Легко показать, что переводится в положение поворотом относительно т. . Доказательство от противного: пусть т. перемещается не в  , а в , причем . Рассматривая треугольники и убеждаемся, что , следовательно, точки  и  совпали.

Любое плоское движение твердого тела можно представить как последовательность бесконечно малых перемещений. При этом некоторые фиксированные точки проходят ряд бесконечно близких последовательных положений. Согласно теореме переход из положения в следующее  осуществляется поворотом вокруг оси , из  в вокруг оси  и т.д. Произвольное плоское движение может быть представлено как вращение вокруг мгновенной оси, движущейся как в теле, так и в пространстве.

Твердое тело, имеющее одну неподвижную точку, смещается из одного произвольного положения в другое поворотом вокруг некоторой оси, проходящей через эту точку. (общая формулировка т. Эйлера).

Из т. Эйлера следует независимость угловой скорости вращения от положения т., относительно которой измеряется вращение твердого тела. В самом деле, рассматривая движение произвольной точки  твердого тела относительно точек  и  (см. рис.n8) имеем: , где  - радиус – вектор из т.  в т. . Аналогично, относительно т. : , где соответственно радиус вектор из т.  в . Приравнивая скорости и подставляя , получаем: . Рассматривая также движение точки  относительно т.  как поступательный сдвиг и вращение имеем: . С учетом этих соотношений находим:

,  отсюда

.

В силу произвольности  - угловые скорости относительно произвольных точек твердого тела одинаковы.

Кинетическая энергия твердого тела.

            Рассмотрим движение произвольного твердого тела которое движется поступательно и вращается относительно некоторой оси. Если вращение рассматривается относительно оси, проходящей через центр масс, то кинетическая энергия такого вращательного движения 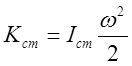. В лабораторной системе отсчета вся кинетическая энергия согласно правилу преобразования кинетической энергии при переходе из одной системы отсчета в другую: 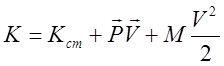,  где - скорость центра масс относительно лабораторной системы отсчета. Учитывая, что в системе центра масс полный импульс , находим:

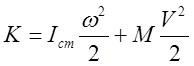.                                      (15)

Кинетическая энергия складывается из энергии вращения твердого тела относительно оси, проходящей через центр масс и энергии поступательного движения тела, как целого сос скоростью центра масс.

Пример. Рассмотрим скатывание тонкостенного обруча массы , радиуса  по наклонной плоскости без проскальзывания.

Пусть изменение высоты центра масс обруча составило . Какую скорость приобретет обруч к этому моменту?

Напишем закон сохранения энергии: . Поскольку начальная кинетическая энергия равна нулю, то, согласно (15) 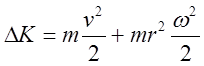, для обруча .

Отсутствие проскальзывания дает: . Подставляя в закон сохранения энергии, получаем: . Для точечной частицы !

Пример 2. Рассмотрим какие нагрузки создает на ось вращающиеся неуравновешенные массы. Рассмотрим вращение некоторой точечной массы, закрепленной на жестком стержне под углом относительно оси вращения. (см. рис. n9). Говорят, что в таком случае масса неуравновешена, создает нагрузки в подшипниках оси.

Подсчитаем момент импульса частицы относительно начала отсчета – т. . Вращение происходит относительно вертикальной оси с угловой скоростью .

.

Видно, что компонента момента импульса вдоль оси вращения - . Что касается проекции на произвольную ось в плоскости поперечной относительно оси компоненты импульса , то очевидно, что она меняется по гармоническому закону, т.к. проекция радиуса частицы  на выбранную ось при равномерном вращении -. Итак . При этом Запишем основное уравнение динамики твердого тела:

.

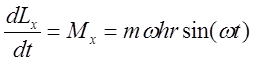Для компенсации момента сил необходимо в подшипниках, на которую опирается ось вращения создавать усилия. Ясно, что будет происходить деформация самой оси вращения.