Определение передаточной функции объекта по кривой разгона методом последовательного логарифмированияккк, страница 5

Рис. 4. График функции “невязки” F 3.

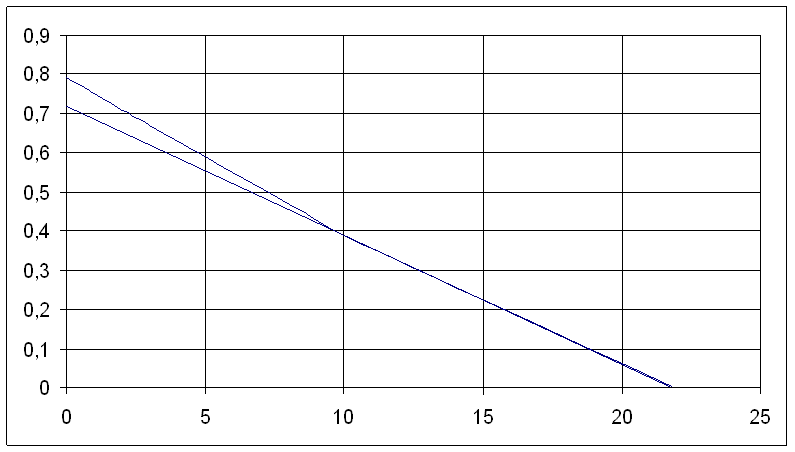
Проводим к хвостовой части касательную А3 этой точке соответствует значение lgC₃=0.72.

откуда С₃=5.24.

При этом t3=21.8 мин.

Определяем α3 как:

α3 =-lg[C3]/0.434*t3= -0.82/0.434*21.8= -0.087.

откуда 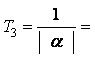1/0.086=11.49 мин.

Следовательно третья составляющая суммы равна:

С₃e^-^t^/^T₃=5.24^-^t^/^11.49.

При малых t lg [f3(t)] не совпадает с А3- находим “невязку” – функцию F4(t)=F3(t)- С3e^α³^t

Строим график функции lg [F4(t)]:

Таблица 4.

1 2 3 4 5 6 7 8 9 10