Движение твердого тела с одной закрепленной точкой

§3.22. Движение твердого тела с одной закрепленной точкой.

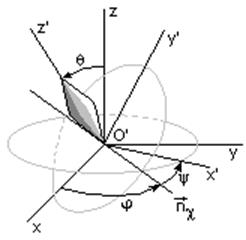
        Ряд очень важных практических приложений связан с механическими устройствами, называемыми гироскопами. Рассмотрим задачу о движении твердого тела с одной закрепленной точкой (задача о тяжелом симметричном волчке). Свяжем с волчком подвижные координаты O’x’y’z’. Для определения положения волчка будем использовать углы Эйлера j, y и q, введенные ранее в кинематике. Масса волчка равна m, расстояние от точки опоры волчка до его центра масс равно l.

            Для решения задачи необходимо записать кинетическую энергию волчка как функцию независимых обобщенных координат j, y и q и их производных по времени:

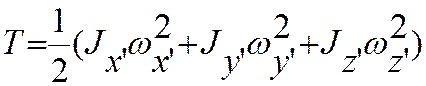             (3.22.1)

            Для движения твердого тела с одной закрепленной точкой имеют место кинематические формулы Эйлера:

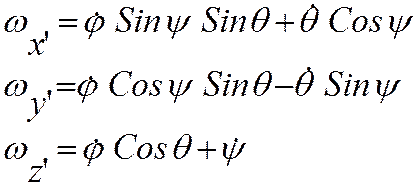              (3.22.2)

            Подставляя (3.22.2) в (3.22.1) будем иметь:

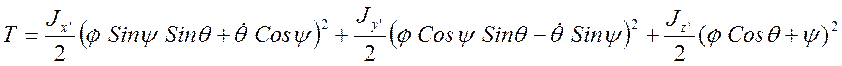            (3.22.3)

            Волчок симметричный (), поэтому выражение (3.22.3) упростится:

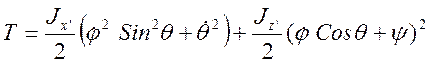
            Функция Лагранжа для нашего волчка будет иметь вид:

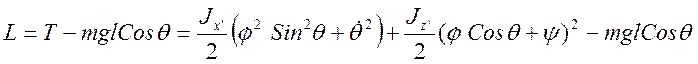            (3.22.4)

            Функция Лагранжа явно от времени и углов j и y не зависит, поэтому можно получить три первых интеграла:

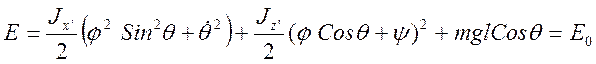         (3.22.5)

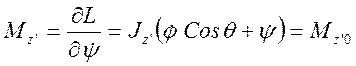            (3.22.6)

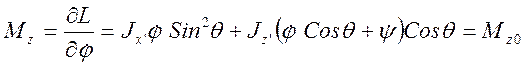         (3.22.7)

Из (3.22.6) и (3.22.7) можно получить:

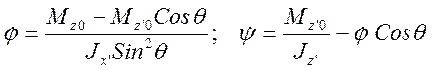            (3.22.8)

Подставляя (3.22.8) в закон сохранения механической энергии (3.22.5) найдем дифференциальное уравнение для  угла q:

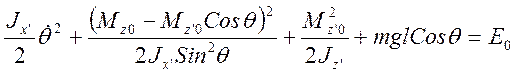          (3.22.9)

            Это уравнение имеет решение в элементарных функциях, если при t=0 наклоненный волчок закручен вокруг своей неподвижной оси симметрии и выполняются условия:

          (3.22.10)

Подставляя (3.22.10) в первые интегралы (3.22.5), (3.22.6) и (3.22.7) получим:

       (3.22.11)

Подставляя теперь (3.22.11) в (3.22.9) найдем:

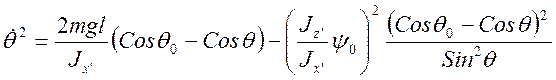;              (3.22.12)

откуда вытекает, что , так как . Это означает, что наклон оси волчка с течением времени может только увеличиться.

            Поскольку мы считаем, что волчок сильно закручен, его кинетическая энергия много больше потенциальной. Это означает, что

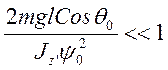
и из (3.22.12) также следует, что в любой момент времени  (q мало отличается от q₀).

            Учитывая это, можно получить приближенное аналитическое решение (3.22.12) разлагая правую часть в окрестности q₀ до членов второго порядка малости включительно:

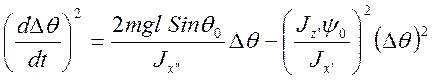;           (3.22.13)

Здесь нельзя пренебречь последним членом в правой части, так как Dq² домножается на большое число.

            Используя обозначения 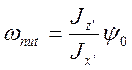 и 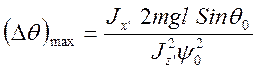 перепишем (3.22.13) в виде:

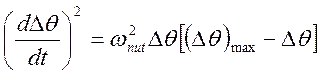;     (3.22.14)

            Решением (3.22.14), удовлетворяющим начальным условиям  является функция

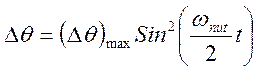
            В конечном итоге можно получить решение для углов Эйлера и их производных по времени:

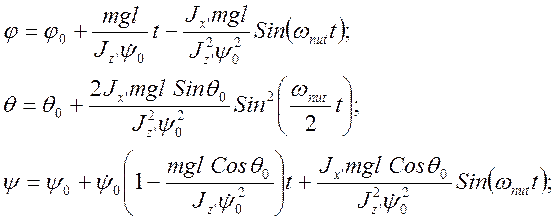               (3.22.15)

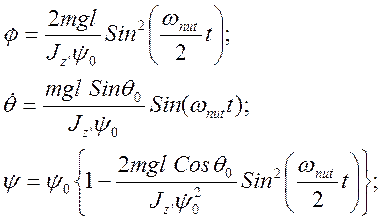                                (3.22.16)

            Выражения для угловых скоростей, усредненных по периоду  имеют вид:

;               (3.22.17)

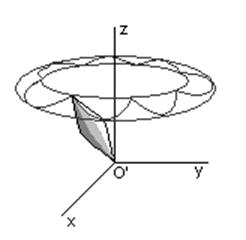            Из решения видно, что ось z’ медленно прецессирует вокруг вертикали со средней угловой скоростью , которая стремится к нулю при стремлении . Угловая скорость  колеблется около среднего значения с малой амплитудой и большой частотой . Одновременно ось волчка колеблется с амплитудой .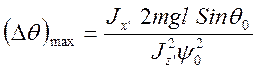

            Таким образом, в среднем получаем картину регулярной прецессии вокруг вертикали, а на это усредненное движение налагается дрожание оси с малой амплитудой, то есть нутация. Такое движение называется псевдорегулярной прецессией.

§3.23. Теория колебаний. Устойчивость положения равновесия.

            Теория колебаний один из самых обширных и развитых разделов теоретической механики, имеющий больное прикладное значение.

            Рассмотрим основные свойства малых колебаний механических систем с одной и двумя степенями свободы на основе применения уравнений Лагранжа. Некоторые результаты для системы с любым  конечным числом степеней свободы приведем без вывода.

            Механическая система может совершать малые колебания только вблизи устойчивого положения равновесия. Обобщенные координаты системы в положении равновесия принимают равными нулю, т.е. отсчитывают их от положения равновесия. Тогда колебательным движением механической системы в общем случае считают всякое ее движение, при котором все обобщенные координаты или часть из них изменяются не монотонно, а имеют колебательный характер, т.е. принимают нулевые значения по крайней мере несколько раз.

Далее будем рассматривать только периодические и псевдопериодические колебания.