Движение твердого тела с одной закрепленной точкой, страница 2

 Положение равновесия может быть устойчивым, безразличным или неустойчивым. Если существует такое достаточно малое начальное отклонение системы от положения равновесия, при котором силы стремятся вернуть систему в положение равновесия, то такое положение равновесия считается устойчивым.

 В том случае, когда силы еще дальше отклоняют систему от положения равновесия, положение равновесия является неустойчивым.

 Если же система, получив любое малое отклонение от положения равновесия, остается в равновесии и в новом отклоненном положении, то такое положение равновесия будем называть безразличным.

 Строгое определение устойчивости было дано в конце 19 века в работах А.М.Ляпунова. Начальное возмущение системы состоит в общем случае из начальных значений обобщенных координат q₁₀,q₂₀,….q_n0 и начальных обобщенных скоростей . По Ляпунову равновесие системы называется устойчивым, если для любого достаточно малого e>0 можно выбрать два других таких малых числа h₁>0 и h₂>0, что при удовлетворении начальными значениями обобщенных координат и скоростей неравенств  в любой момент времени все обобщенные координаты подчиняются условиям .

 В положении равновесия механической системы каждая обобщенная сила Q_i равна нулю. Для случая потенциального силового поля обобщенные силы вычисляются через потенциальную  энергию по формулам

 Следовательно, в положении любого равновесия  и потенциальная энергия достигает своего экстремального значения.

 Малые колебания системы могут длительно совершаться только в окрестности устойчивого положения равновесия системы. В соответствии с теоремой Лагранжа-Дирихле для этого достаточно, чтобы потенциальная энергия в положении равновесия имела изолированный относительный минимум.

§3.24. Теория колебаний. Собственные колебания системы с одной степенью свободы.

Механическая система с одной степенью свободы имеет одну обобщенную координату q, и ее движение описывается одним уравнением Лагранжа

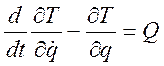.        (3.24.1)

Обобщенную силу можно Q считать состоящей из трех частей: Q=Q^П+Q^Ф+Q^B. Здесь Q^П-обобщенная сила потенциальных сил, в Q^Ф включена та часть обобщенной силы, которая получается от действия сил сопротивления, зависящих как от числовых значений, так и направлений скоростей точек системы. В дальнейшем будем рассматривать случай линейного сопротивления, когда силы сопротивления точек системы пропорциональны скоростям этих точек и направлены в стороны, противоположные скоростям.

Часть обобщенной силы Q^B получается от так называемых вынуждающих, или возмущающих, сил, зависящих прежде всего от времени. Мы будем рассматривать случай гармонической возмущающей силы, а в общем случае зависимость этой возмущающей силы от времени можно разложить в ряд Фурье и рассматривать дифференциальные уравнения движения для каждого из синусоидальных слагаемых.

Сначала рассмотрим малые собственные колебания системы с одной степенью свободы под действием потенциальных сил (Q=Q^П= ). Сил сопротивления и возмущающих сил нет. Колебания считаются малыми, если при движении системы обобщенная координата, скорость и ускорение достаточно малы и в уравнении Лагранжа (3.24.1) можно пренебречь всеми слагаемыми второго и более высокого порядков относительно  при разложении величин Т и П в ряды.

Можно показать, что при принятых допущениях для кинетической энергии Т в малой окрестности положения равновесия мы будем иметь в нашей задаче

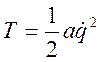;                  (3.24.2).

Здесь положительная постоянная a называется коэффициентом инерции и обычно по размерности является или массой  (m) или моментом инерции.

Разлагая потенциальную энергию в степенной ряд в окрестности q=0 получим

 .

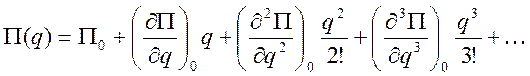Потенциальную энергию П₀ в положении равновесия при q=0 примем равной нулю. Величина 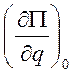есть значение обобщенной силы Q в положении равновесия системы, равное нулю.

Будем считать, что в положении равновесия потенциальная энергия имеет минимум. Это является достаточным условием устойчивости положения равновесия. В этом случае величина 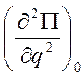положительна, обозначим ее с (часто ее называют коэффициентом жесткости). Таким образом, отбрасывая слагаемые третьего и более высоких порядков, имеем

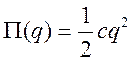.             (3.24.3)

Системы, для которых кинетическая и потенциальная энергия выражаются точно по формулам (3.24.2) и (3.24.3) без отбрасывания слагаемых более высокого порядка, называются линейными. Для них вся математическая теория является такой же, как и для систем, совершающих малые колебания, хотя колебания для линейных систем могут быть любыми, не обязательно малыми.