Задача синтеза фильтра с фиксированной структурой (2.23) подробно рассмотрена в работе [36], а на рисунке 2.18 представлено основное окно расчётов при синтезе компенсаторов. Слева от поля вывода графиков представлены значения весовых коэффициентов синтезируемого фильтра, hf(iTS), которые используются в алгоритмическом модуле цифровой обработки информации виртуального прибора. Фильтры с фиксированной структурой (2.23) широко используются в безмодельных робастных системах, так как решение принимается по текущей измерительной информации. Поэтому требования к качеству измерительной информации резко возрастают. Это важно и для робастных систем с эталонной математической моделью, когда критерием управления является эффективность процесса управления. Он же являются обобщенным технологическим параметром и, как правило, является нелинейной функцией (КПД, степень насыщения, себестоимость и т. д.). При вычислении текущих значений этих параметров участвуют как входные, так и выходные координаты объекта управления и, поэтому, требуется не только приведение результатов измерения к одному моменту времени, но и линеаризация критерия управления. Фиксированная структура фильтров помех измерения, так же проста в процессе пуско-наладочных работ и эксплуатации системы управления.
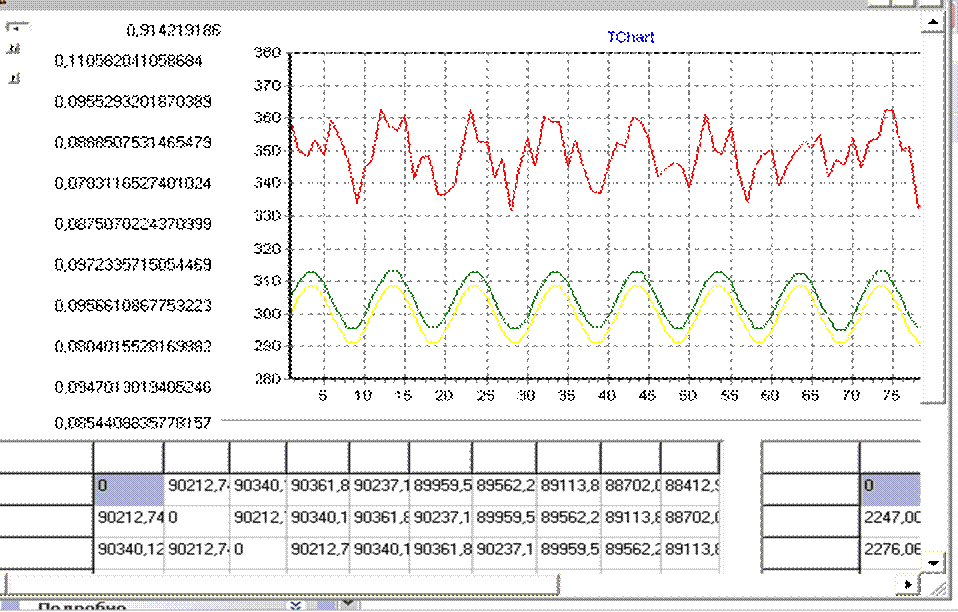
Рис.2.18 АРМ для синтеза фильтров фиксированной структуры
Задача текущей идентификации фильтров произвольной структуры, hf(iTs), в информационно-измерительных подсистемах робастных систем сводится к задаче поиска минимума дисперсии ошибки цифровой обработки информации в постановке:
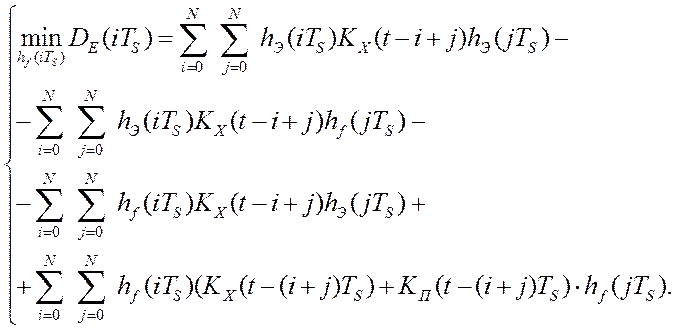
где hf(iTS ) – массив весовых коэффициентов фильтра произвольной структуры, hЭ(iTs) – массив весовых коэффициентов динамической характеристики эталонного фильтра, КX(i,j), KП(i,j) – соответственно, автокорреляционные матрицы входного, обычно возмущающего воздействия и аддитивной помехи измерения наложенной на него, N – длина массивов. При решении этой задачи допущения, ограничения и начальные условия выглядят следующим образом:
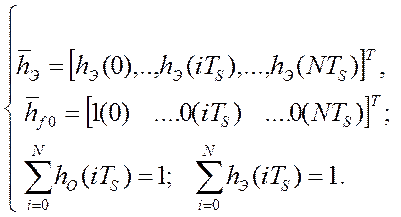
Требования к автокорреляционным матрицам входных параметрах и помехи так же общеизвестны. Они должны быть симметричны относительно диагонали матрицы и не нарушать чётных свойств моделей сигнала и помехи [58]:
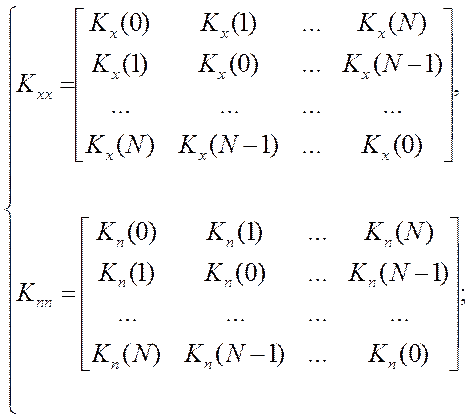
Таким образом, алгоритм текущей идентификации фильтров произвольной структуры сводится к задаче нелинейного программирования и решается методом покоординатного поиска минимума [36]. Структура пакета прикладных программ виртуального прибора для реализации алгоритма синтеза фильтров с произвольной структурой хорошо представлена в работе [36] . В работе [58] показано, что при использовании экспоненциальных моделей сигналов и помехи, наиболее рациональной является процедура покоординатного поиска минимума. Результатом работы алгоритма идентификации является массив весовых коэффициентов фильтра с произвольной структурой, hf(iTS), который используется в программно-аппаратном измерительном канале виртуального прибора. На рисунке 2.19 представлено окно расчётов и форма вывода результатов пакета прикладных программ для синтеза фильтра с произвольной структурой в момент формирования корреляционной матрицы. В результате работы программы в поле экрана отображается реализация измеряемого сигнала, искаженного помехой, реализация помехи и результат сглаживания искаженного сигнала с помощью синтезируемого фильтра с произвольной структурой. Числовые таблицы автоматизированного рабочего места содержат значения ненормированной автокорреляционной функции измеряемого сигнала KXX(t) и ненормированной автокорреляционной функции помехи KП(t). Пакет прикладных программ позволяет ставить и решать задачи синтеза программных фильтров и компенсаторов с произвольной структурой как задачу минимизации методической динамической составляющую погрешности текущей идентификации. Основной отличительной чертой этих задач является возможность их решения в реальном масштабе времени при условии, что автокорреляционные функции измеряемого сигнала и помехи имеют экспоненциальный вид. То есть, измеряемый параметр является случайным процессом со свойствами стационарности и эргодичности.
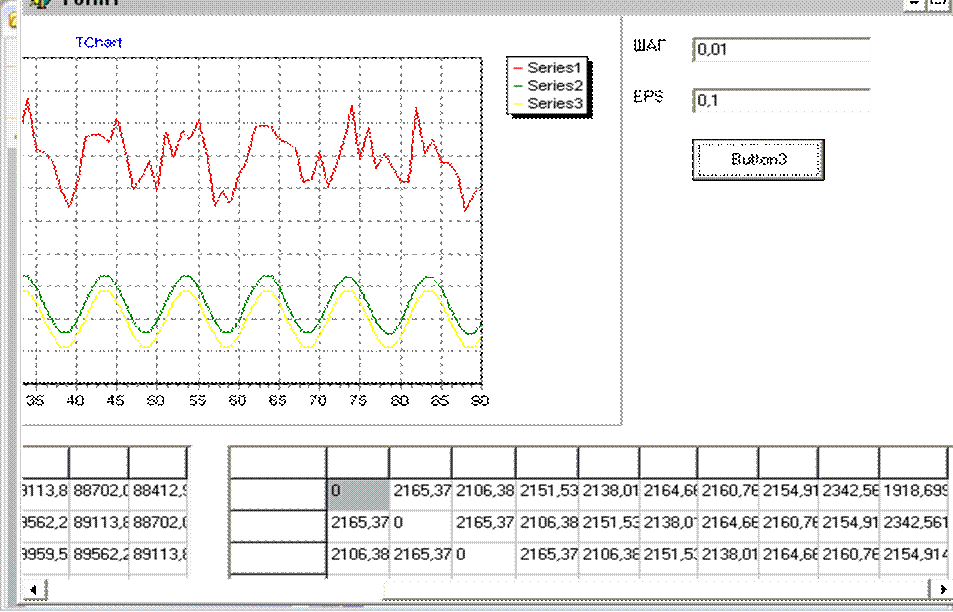
Рис. 2.19 АРМ для синтеза фильтров произвольной структуры
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.