где Ak - коэффициенты линеаризации, k – порядковый номер программно-аппаратного измерительного канала.
Динамические преобразования измерительной информации широко применяются при управлении техническими системами как для фильтрации помех, так и для компенсации динамических свойств объектов управления. Один из наиболее распространённых, вследствие простоты реализации, оптимальных фильтров, применяемых для первичной фильтрации измеряемого сигнала от помех в типовом алгоритмическом модуле (см. рис. 2.17), имеет вид рекуррентного соотношения:
Y(iTS) = Y{(n –
1)TS} + TS/![]() [X(iTS) –
Y{(i – 1)TS}], (2.23)
[X(iTS) –
Y{(i – 1)TS}], (2.23)
где Y(iTS) – текущее значение выходного сигнала фильтра в
момент времени iTS;
X(iTS) – текущее значение входного сигнала
фильтра; Y{(n–1)} – значение выходного
сигнала фильтра в предыдущий момент времени; ![]() – постоянная
времени программного фильтра; TS – период опроса датчиков.
– постоянная
времени программного фильтра; TS – период опроса датчиков.
Фильтр с фиксированной структурой (2.23) обеспечивает во многих случаях удовлетворительное качество фильтрации, прост в реализации и требует небольших объёмов памяти ЭВМ.
Вместе с этим, наиболее эффективным методом фильтрации является фильтрация с помощью фильтра произвольной структуры.
Фильтр произвольной структуры рекомендуется применять для сигналов на выходе объекта и, как правило, характеризующихся интенсивными помехами со стороны параметров возмущения, F(t), приводящих к дрейфу критерия управления. Алгоритм фильтрации имеет вид соотношения:
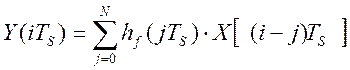 , (2.24)
, (2.24)
где hf(iTS) – массив весовых коэффициентов фильтра.
Большое значение при реализации типового алгоритмического модуля имеет компенсатор динамических свойств объекта управления с фиксированной структурой. Он необходим для обработки входных переменных объекта управления и приведения их к одному моменту времени измерения с выходными переменными [58]:
Y(iTS) = Y{(n – 1)TS} + TS/TO [X(iTS) – Y{(i – 1)TS}], (2.25)
где To– постоянная времени объекта управления.
Компенсатор с произвольной структурой применяется для реализации алгоритмов управления с компенсацией возмущений в сочетании с текущей идентификацией динамических характеристик объекта управления, применяемых для реализации виртуальных приборов. Компенсатор с произвольной структурой имеет вид:
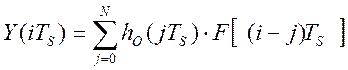 (2.26)
(2.26)
где F(iTS) – текущие значения возмущающего параметра, измеряемого на входе динамического объекта; Y(iTS) – текущие значения критерия управления; ho (iTS) – i– тый элемент массива весовых коэффициентов динамической характеристики объекта управления.
Постановка задачи синтеза фильтров для информационно-измерительной подсистемы сводится к задаче поиска минимума дисперсии ошибки цифровой обработки измерительной информации по критерию [36]:
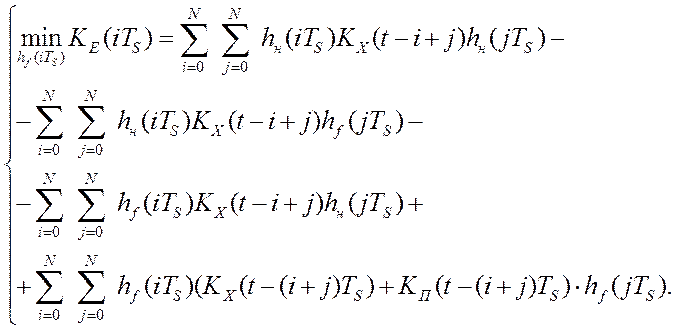
где hf(iTS) – массив весовых коэффициентов динамической характеристики синтезируемого фильтра, hн(iTs) – массив весовых коэффициентов динамической характеристики эталонного фильтра, КX(i,j), KП(i,j) – соответственно, автокорреляционные матрицы измеряемого сигнала и аддитивной помехи измерения, N – длина массивов. При решении этой задачи допущения и ограничения выглядят следующим образом:
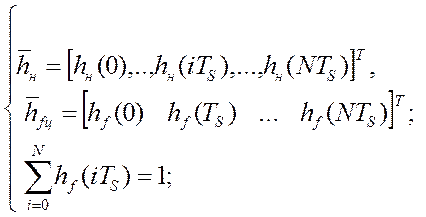
Для обеспечения хорошей обратимости корреляционных матриц они должны быть симметричны относительно диагонали матрицы и не нарушать чётные свойства моделей сигнала и помехи [58].
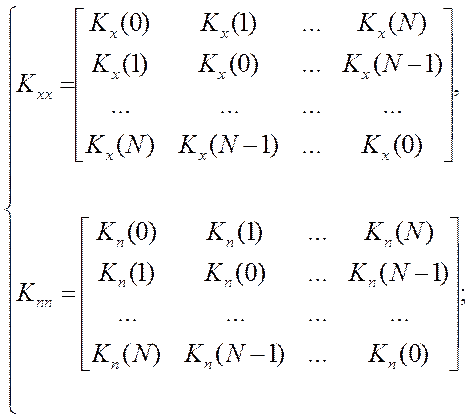
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.