Алгоритмы первичной обработки измерительной информации (Раздел 2.2 учебника "Планово-экономическое управление"), страница 4

где T_S – период опроса датчиков; i – порядковый номер дискретного времени в решётчатой функции; E[…] – целая часть числа.

             В качестве обобщенной весовой функции эталонного преобразования измеряемой величины, X(t) в показаниях эталонного прибора, Y(t) будем использовать выражение вида:

                                                      ,               (2.15)                    

где К_н – коэффициент передачи эталонного измерительного канала, d(t) – функция Дирака [20].

 Основным назначением операции перевода в требуемые единицы измерения является компенсация статических преобразований, осуществляемых над измеряемым сигналом в первичном и нормирующем преобразователях. Для последовательного соединения преобразователей с весовыми функциями (2.14) и (2.15) блок реализации шкалы датчика может быть описан в виде звена с весовой функцией вида [58 Лясин, Д.Н. Оптимизация параметров линейных программно-аппаратных измерительных каналов в АСУ ТП [Текст] / Д.Н. Лясин, C.И. Данилов, В.П. Шевчук; ВолгГТУ. - Волгоград, 1999. - 19 с. - Деп. в ВИНИТИ 10.06.99, № 1883 - В99.]:

.

(2.16)

            В качестве модели последовательности,Y₁(iT_S), на выходе  алгоритмического модуля цифровой обработки информации (см. рис. 2.17) будем использовать последовательность прямоугольных импульсов:

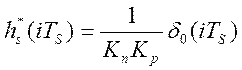                                                ,                            (2.17)

где .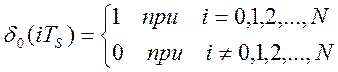

          Динамические преобразования в цифровой части программно-аппаратного измерительного канала целесообразно проводить с помощью рекуррентного соотношения, которое определяет массив текущих значений на выходе программного динамического преобразователя Y(iT_S) как функцию текущих значений массива измеряемой величины X(iT_S) и предыдущих  значений массива на  выходе программного динамического преобразователя Y{(n-1)T_S}. То есть в разностной форме записи дифференциального уравнения первого порядка:

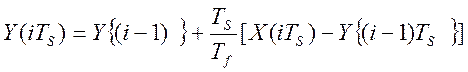                          ,                  (2.18)

здесь T_S– интервал времени между двумя соседними измеренными значениями  (период опроса датчиков).

          Весовая функция такого программного динамического преобразования может быть получена из рекуррентного уравнения (2.18) путем применения дискретного преобразования Лапласа [20] :

                ,

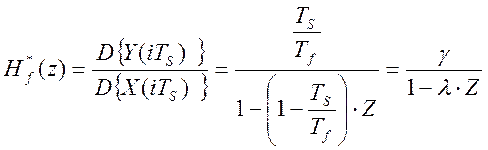где: 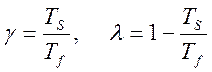. Тогда весовая функция программного преобразователя, определяемая как обратное дискретное преобразование Лапласа от передаточной функции модели (2.18) и будет равна:

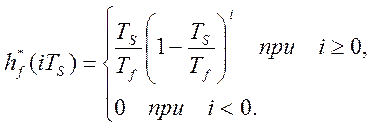                                           (2.19)

где i - целые число от 0 до N.                    

          Весовая функция восстанавливающего элемента (регистратора) может быть описана [7, 10] прямоугольным импульсом длительностью T_s и амплитудой, равной 1/T_s :

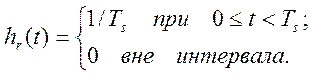                                                              (2.20)

Восстановление сигналов (преобразование его из дискретной в аналоговую форму) для представления потребителю информации удобно осуществлять методом ступенчатой экстраполяции, когда о значении измеряемой величины в некоторый момент времени t судят по предшествующему этому времени замеру kTs, для которого k=E[t/Ts]. Алгоритм функционирования такого восстанавливающего элемента можно описать выражением [58 Острем, К. Системы управления с ЭВМ [Текст] / К. Острем. - М.: Мир, 1987. – 480 с.]:

                      ,

где Z(t) – восстановленная, модулем вывода (МВВА) аналоговая информация; G(iT_S) – измеряемый сигнал на входе      в программно-аппаратный измерительный канал (см. рис. 3.1); i – порядковый номер измерения.

         В состав измерительных каналов линеаризованной эталонной системы входят, дополнительно, два компонента. Первым является динамический компенсатор с весовой функцией:

.

(2.21)

Вторым компонентом эталонной измерительной системы является усилительное звено с весовой функцией:

                                           ,                                          (2.22)