


































Розділ 7
Чисельне інтегрування функцій
Задача чисельного інтегрування функції полягає в обчисленні наближеного значення визначеного інтеграла
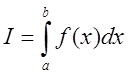
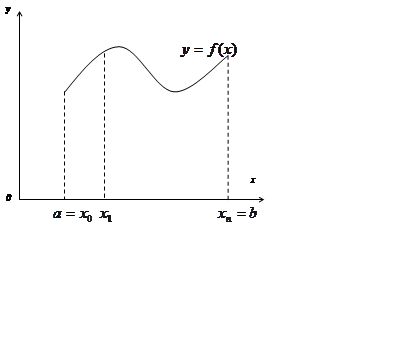 з
використанням значень підінтегральної функції
з
використанням значень підінтегральної функції ![]() у
вузлах сітки
у
вузлах сітки ![]() . Визначений інтеграл
. Визначений інтеграл ![]() представляє площу криволінійної трапеції,
обмеженої кривою у=
представляє площу криволінійної трапеції,
обмеженої кривою у=![]() , віссю
, віссю ![]() та прямими
та прямими ![]() та
та ![]() .
.

Рис. – 7.1
У практичних розрахунках нерідко виникає потреба в обчисленні визначених інтегралів вигляду
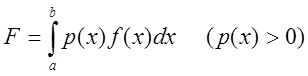 ,
,
де функція ![]() та вагова функція
та вагова функція ![]() неперервні
на відрізку
неперервні
на відрізку ![]() .
.
До
чисельного інтегрування вдаються тоді, коли інтеграл неможливо виразити через
елементарні функції або ж функція ![]() задана таблично, а також
коли внаслідок інтегрування одержано незручний для використання вираз. Тоді
задана таблично, а також
коли внаслідок інтегрування одержано незручний для використання вираз. Тоді ![]() наближають більш зручною функцією
наближають більш зручною функцією ![]() .
.
Найчастіше
підінтегральну функцію ![]() заміняють на деякий узагальнений
поліном. Тоді внаслідок лінійності такої апроксимації функцію
заміняють на деякий узагальнений
поліном. Тоді внаслідок лінійності такої апроксимації функцію ![]() можна записати так:
можна записати так:
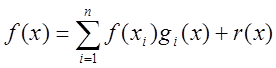 ,
,
де ![]() - залишковий член апроксимації. Підставивши
вираз
- залишковий член апроксимації. Підставивши
вираз 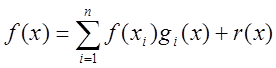 у формулу
у формулу 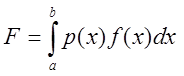 ,
одержимо загальну формулу чисельного інтегрування – квадратурну формулу
,
одержимо загальну формулу чисельного інтегрування – квадратурну формулу
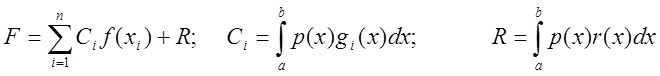 ,
,
де ![]() вузли;
вузли; ![]() - ваги;
- ваги; ![]() похибка або залишковий член квадратурної
формули.
похибка або залишковий член квадратурної
формули.
Отже,
інтеграл наближено замінено на суму, подібну до інтегральної, причому як вузли,
так і коефіцієнти (ваги) квадратурної формули не залежать від функції ![]() .
.
Будемо
будувати формулу чисельного інтегрування за правилом 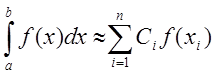 .
.
Це
відношення називається квадратурною формулою. При цьому: права частина виразу 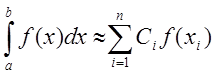 називається квадратурною сумою. Тут
називається квадратурною сумою. Тут ![]() параметри квадратурної формули:
параметри квадратурної формули:![]() квадратурні (вагові) коефіцієнти;
квадратурні (вагові) коефіцієнти;![]() квадратурні вузли.
квадратурні вузли.
Якщо
межі інтегрування ![]() являються квадратурними вузлами,
то отримуємо формулу замкненого типу. Інакше маємо квадратурну формулу
відкритого типу.
являються квадратурними вузлами,
то отримуємо формулу замкненого типу. Інакше маємо квадратурну формулу
відкритого типу.
Величина
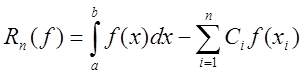 називається похибкою квадратурної формули
називається похибкою квадратурної формули 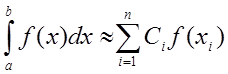 .
.
Якщо
для деякої функції ![]() маємо
маємо ![]() то
квадратурна формула являється для даної функції точною.
то
квадратурна формула являється для даної функції точною.
Квадратурна
формула 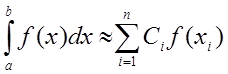 має алгебраїчний степінь точності
має алгебраїчний степінь точності ![]() , якщо вона є точною при
, якщо вона є точною при ![]() і не точною при
і не точною при ![]()
Звідси
очевидно, що квадратурна формула степеня точності ![]() є
точною для всіх алгебраїчних многочленів степеня не вище за
є
точною для всіх алгебраїчних многочленів степеня не вище за ![]() , причому число
, причому число ![]() - максимальний
степінь таких многочленів.
- максимальний
степінь таких многочленів.
Визначимо
верхню оцінку точності для формули 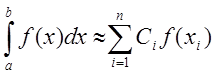 при фіксованому
при фіксованому ![]()
Лема. Степінь точності формули 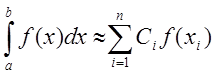 не може бути вище за
не може бути вище за ![]() при будь-якому виборі параметрів
при будь-якому виборі параметрів ![]()
Доведення Розглянемо довільну квадратурну
формулу 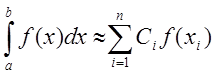 . Нехай
. Нехай ![]() Це
многочлен степеня
Це
многочлен степеня ![]() . Оскільки
. Оскільки ![]() то
то 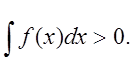 З
іншого боку,
З
іншого боку, 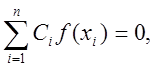 тобто формула
тобто формула 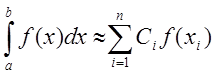 в даному випадку не є точною.
в даному випадку не є точною.
Формули чисельного обчислення однократного інтеграла називаються квадратурними формулами, подвійного й більшої кратності - кубатурними.
Наближеним значенням інтеграла будемо
вважати вираз 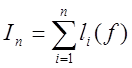 , де
, де ![]() –
наближене значення інтеграла на частковому відрізку
–
наближене значення інтеграла на частковому відрізку ![]() . При
цьому формула для обчислення
. При
цьому формула для обчислення ![]() називається найпростішою
квадратурною формулою, а формула для обчислення
називається найпростішою
квадратурною формулою, а формула для обчислення ![]() – складеною
квадратурною формулою.
– складеною
квадратурною формулою.
7.1 Квадратурні формули Ньютона-Котеса
Розглянемо формули для наближеного обчислення інтегралів
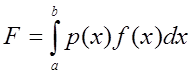 . (7.1)
. (7.1)
Обмежимося випадком, коли ![]() . Цей метод заснований на заміні
підінтегральної функції інтерполяційним многочленом Лагранжа з вузлами, що
розбивають відрізок
. Цей метод заснований на заміні
підінтегральної функції інтерполяційним многочленом Лагранжа з вузлами, що
розбивають відрізок ![]() на рівні частини. Такі формули
називаються формулами Ньютона-Котеса.
на рівні частини. Такі формули
називаються формулами Ньютона-Котеса.
Отже,
нехай задана рівномірна сітка ![]() ,
, ![]() ,
, ![]() . Тобто
крок
. Тобто
крок 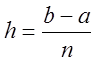 – величина постійна й розбиває відрізок
– величина постійна й розбиває відрізок ![]() на
на ![]() рівних
інтервалів. Формули Ньютона-Котеса - формули замкненого типу. Позначимо
рівних
інтервалів. Формули Ньютона-Котеса - формули замкненого типу. Позначимо ![]() . За наближену функцію
. За наближену функцію ![]() оберемо інтерполяційний поліном Лагранжа
оберемо інтерполяційний поліном Лагранжа
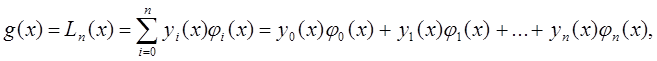 де
де 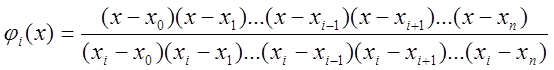 .
.
Отже, заданий інтеграл може бути поданий у вигляді
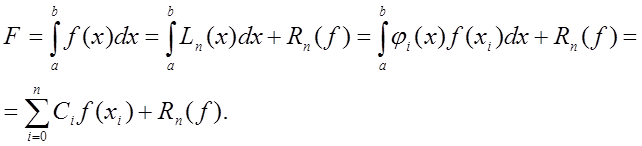
Таку квадратурну формулу називають квадратурною формулою інтерполяційного типу.
Нехай 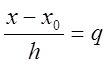 –
виражена в сіткових кроках довжина
–
виражена в сіткових кроках довжина ![]() . Тоді
. Тоді
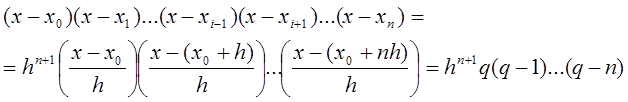
![]() ;
;
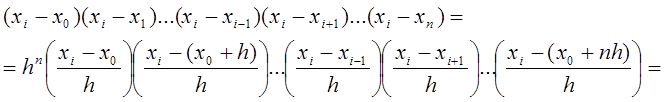
![]() .
.
У такому випадку ваги можна розрахувати так:
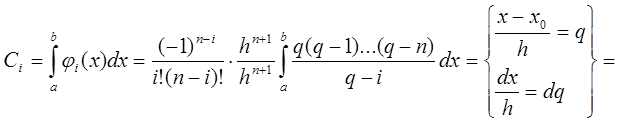
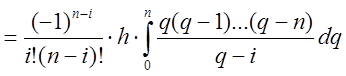 .
(7.2)
.
(7.2)
Формула (7.2) остаточно визначає ваги
квадратурної формули Ньютона-Котеса. Замінимо в ній 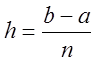 і
введемо позначення
і
введемо позначення ![]() . Тоді коефіцієнти
. Тоді коефіцієнти
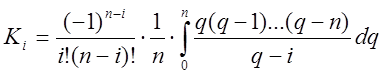 (7.3)
(7.3)
називаються коефіцієнтами Котеса. А сама квадратурна формула Ньютона-Котеса набирає вигляду
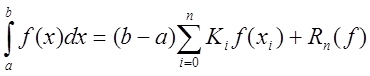 . (7.4)
. (7.4)
Для коефіцієнтів Котеса мають місце співвідношення:
1 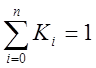 .
.
2 ![]() .
.
З’ясуємо питання про степінь точності квадратурної формули  .
.
Нехай
![]() алгебраїчний многочлен степеня не вищого
за
алгебраїчний многочлен степеня не вищого
за ![]() . Тоді, згідно з властивостями інтерполяції
. Тоді, згідно з властивостями інтерполяції
![]() , тобто
, тобто ![]() Таким
чином, інтерполяційна квадратурна формула
Таким
чином, інтерполяційна квадратурна формула  має
степінь точності не нижчий за
має
степінь точності не нижчий за ![]() .
.
Звідси
можна зробити висновок, що квадратурні коефіцієнти ![]() формули
формули
 є єдиним розв’язком лінійної системи
рівнянь
є єдиним розв’язком лінійної системи
рівнянь
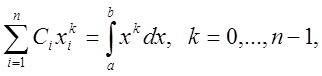
яка отримана із  при
при ![]()
Розглянемо
окремі випадки квадратурних формул Ньютона-Котеса з рівновіддаленими вузлами, в
яких підінтегральна функція ![]() замінена на
інтерполяційний поліном Лагранжа різного степеня.
замінена на
інтерполяційний поліном Лагранжа різного степеня.
Якщо
на відрізку ![]() взяти єдиний вузол квадратурної формули
взяти єдиний вузол квадратурної формули ![]() , то підінтегральна функція
, то підінтегральна функція ![]() апроксимується поліномом нульового степеня
– сталою
апроксимується поліномом нульового степеня
– сталою ![]() . У зв’язку з тим, що симетричне розміщення
вузлів у чисельному диференціюванні привело до підвищення точності, за вузол
. У зв’язку з тим, що симетричне розміщення
вузлів у чисельному диференціюванні привело до підвищення точності, за вузол ![]() візьмемо середину відрізка інтегрування
візьмемо середину відрізка інтегрування 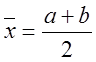 . Замінивши наближено площу криволінійної
трапеції на площу прямокутника з висотою
. Замінивши наближено площу криволінійної
трапеції на площу прямокутника з висотою ![]() та
основою (b- a),
одержимо формулу середніх
та
основою (b- a),
одержимо формулу середніх
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.