Чисельне інтегрування функцій. Квадратурні формули Ньютона-Котеса. Квадратурна формула Гауса, страница 4

У зв'язку з цим широкого застосування набуло правило Рунге апостеріорної оцінки похибки, суть якого полягає в тому, щоб, організувавши обчислення двох значень інтеграла на двох множинах вузлів, їх порівняти й одержати оцінку похибки. Найпоширеніше обчислення інтеграла двічі - із кроками  та .

Якщо 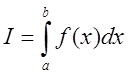 – точне значення інтеграла,  – його наближене значення, обчислене з кроком , а  – наближене значення інтеграла, обчислене із кроком , то похибки кожної квадратурної формули із кроком  і  можна записати відповідно у вигляді ,  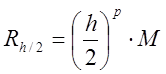          , де  – порядок точності формул. Обчислимо наближене значення інтеграла за однією квадратурною формулою спочатку із кроком , а потім із кроком . Одержимо

,          .

; .

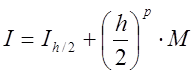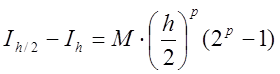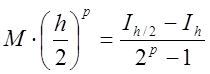Одержали оцінку похибки методом Рунге

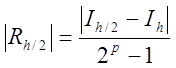.                       (7.13)

Користуючись цією формулою можна уточнити наближене значення інтеграла

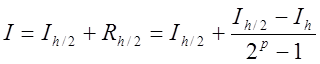.              (7.14)

Цю формулу називають формулою екстраполяції за Річардсоном.

Для формули Симпсона  .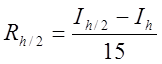

7.4 Вибір квадратурних формул

чисельного інтегрування

Ми одержали ряд формул чисельного інтегрування. Виникають запитання: яку формулу потрібно застосовувати в тому або іншому випадку, які формули більш вигідні і які менш вигідні. На ці питання не можна відповісти однозначно. Усе залежить від того, яким способом задана підінтегральна функція, які обчислювальні засоби використовуються, яка необхідна точність і таке інше.

У такій загальній постановці питання відповісти можна лише так: та формула краща, що у даному випадку дає відповідь з потрібною нам точністю при якомога менших витратах праці і часу.

Якщо обчислення ведуться вручну або за допомогою малих обчислювальних машин, то мають значення формули, що містять різниці. Менш вживані формули Гауса і Чебишева, тому що обчислення з багатозначними коефіцієнтами й абсцисами в цьому випадку є громіздкими. З формул, що не містять різниці, найчастіше застосовується формула Симпсона.

При обчисленнях з використанням сучасних комп’ютерів найуживанішими є безрізницеві формули. Особливо вигідні найбільш точні формули Гауса, тому що вони вимагають найменшого числа операцій для одержання інтеграла з потрібною точністю.

Тут необхідно зробити деякі зауваження щодо більш точних і менш точних формул. Ці терміни були введені нами при виведенні формул чисельного інтегрування й у них вкладався певний зміст. Потрібно чітко розуміти, що більш точна в цьому змісті формула не завжди дає практично більш точний результат. Справді, візьмемо найбільш точну з формул - формулу Гауса . Вона має вигляд

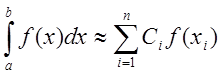,                     (7.15)

де коефіцієнти С_i і абсциси x_i фіксовані і залежать тільки від n і [а,b]. Може трапитися, що підінтегральна функція набуває  нульового значення у кожній із точок х_i, а абсолютна величина  інтеграла від неї велика. Тоді різниця між точним значенням інтеграла і наближеним, отриманим за формулою Гауса, буде також дуже велика. У зв'язку з цим  потрібно відзначити, що при виборі тієї або іншої формули чисельного інтегрування буває доцільно вивчити поводження підінтегральної функції і порівняти його з поводженням інтерполяційного многочлена, інтегруванням якого і знаходиться формула чисельного інтегрування. Іноді виникає необхідність розбивати відрізок інтегрування на окремі ділянки так, щоб краще описати поводження функції інтерполяційними многочленами.

Стосовно вибору квадратурних формул, то, очевидно, що за існування четвертої неперервної похідної від підінтегральної функції  краще користуватися формулою парабол, за існування лише другої похідної та аналітичного задання  - формулою середніх, а за табличного–формулою трапеції. Для функції  високої гладкості найзручнішою є формула Гауса.

Оскільки узагальнені формула середніх і формула трапецій є інтегральними сумами, вони мають збігатися до точного значення інтеграла для довільної неперервної функції. Сказане має місце і для формули парабол (оскільки формула парабол – комбінація формули середніх і формули трапеції). Можна довести збіжність і квадратурної формули Гауса.