Чисельне інтегрування функцій. Квадратурні формули Ньютона-Котеса. Квадратурна формула Гауса, страница 7

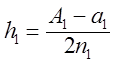Нехай  і 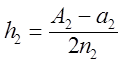. Тоді мережа вузлів буде мати координати:           ;

                             

Для скорочення введемо позначення

Застосовуючи формулу (7.24) до кожного із прямокутників великої мережі, будемо мати (рис.7.7):

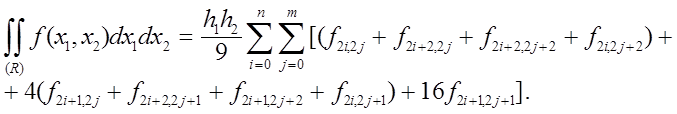Звідси, виконавши зведення подібних членів, остаточно знаходимо:

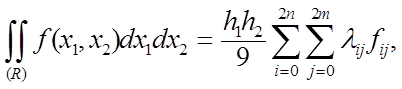      (7.26)

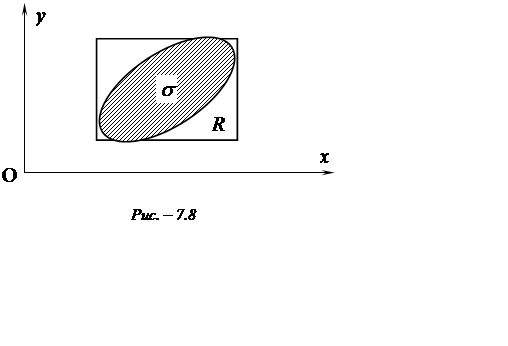
де коефіцієнти  є відповідними елементами матриці

Якщо область інтегрування  – довільна, то будуємо паралелепіпед , сторони якого паралельні осям координат (рис. 7.8). Розглянемо допоміжну функцію

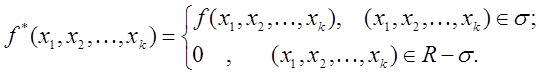
У такому випадку маємо

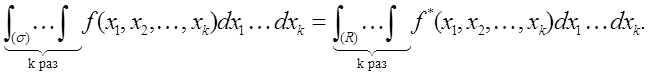            Останній інтеграл приблизно може бути обчислений за загальною кубатурною формулою (7.26).

Питання і завдання до розділу 7

1  Найпростіші квадратурні формули ( прямокутників, трапецій, Симпсона), геометрична ілюстрація, оцінки похибки.  Точність квадратурних формул.

2  Квадратурні формули інтерполяційного типу: виведення формул, оцінки похибки.

3  Квадратурні формули Гауса: виведення формул, точність формул.

4  Правило Рунге практичної оцінки похибки. Адаптивні процедури чисельного інтегрування.

5  Обчислити наближено з кроком h=1 інтеграл 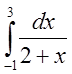 за формулами прямокутників, трапецій, Симпсона. Оцінити похибку теоретично.

6  Переконатися в тім, що формула прямокутників є точною для многочленів , а формула Симпсона – для многочленів .

7  Оцінити теоретично значення кроку інтегрування h для наближеного обчислення  інтеграла 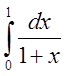 за формулою трапецій з точністю .

8  Оцінити теоретично значення кроку інтегрування h для наближеного обчислення інтеграла 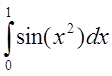 по формулі Симпсона з точністю .

9  Одержати квадратурні формули прямокутників і трапецій із загальної формули інтерполяційного типу.

10  Переконатися, що квадратурна формула Гауса з одним вузлом точна для многочленів .

11  Обчислити інтеграл 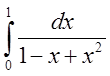  за формулами трапецій і Симпсона з точністю , використовуючи правило Рунге оцінки похибки.

12  Знайти оцінку похибки обчислення інтеграла 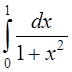 за складеною формулою

.

13  Оцінити мінімальне число розбиттів відрізка N інтегрування  для наближеного обчислення інтеграла 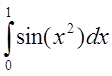 за складеною формулою трапецій, що забезпечує точність .

14 Обчислити інтеграли 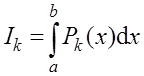, де 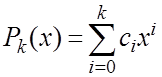, k=0,1,...,5 аналітично й використовуючи квадратурну формулу Симпсона із кроком h = (b-a)/2. Для многочленів якого степеня використовувана квадратурна формула точна й чому? Оцінити похибку інтегрування за правилом Рунге.

15 Обчислити значення інтеграла 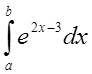  аналітично й,  використовуючи формулу прямокутників із кроками : 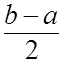, ,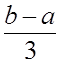…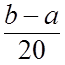...(). При зазначених значеннях  знайти абсолютну похибку й оцінки теоретичної абсолютної похибки. На одному кресленні побудувати графіки знайдених похибок.

16 Побудувати графік функції 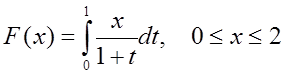. Для обчислення інтеграла з точністю 10^-8  використати квадратурну формулу трапецій і правило Рунге оцінки похибки.

17 Обчислити значення інтеграла  із задачі 14, використовуючи квадратурну формулу Гауса з одним, двома, трьома, чотирма вузлами. Визначити абсолютну похибку результату. Побудувати гістограму залежності похибки від числа вузлів. Переконатися, що квадратурні формули Гауса з N+1 (N=0,1,2,3) вузлами точні для многочленів  1, t,…,t^m, де m=2N+1.

18 Обчислити наближено площу фігури, обмеженої кривими Точки перетину кривих знайти графічно. Для обчислення інтегралів з точністю 10^-8  використати квадратурну формулу Симпсона і правило Рунге оцінки похибки.

19 Наближено обчислити подвійний інтеграл по прямокутній області  з точністю 0.001.

20  Функція  y=y(x)  задана таблицею своїх значень:

x	0	0.1	0.2	0.3	0.4
y	1	1.2	1.24	0.76	0.6

      Обчислити наближене значення інтеграла 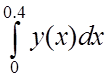 за квадратурними формулами трапецій і Симпсона.

21 Побудувати квадратурну формулу 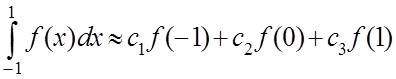, точну для многочленів найбільш високого степеня, використовуючи метод невизначених коефіцієнтів.

22 Знайти наближене значення інтеграла 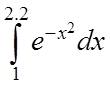 із кроком , використовуючи квадратурні формули прямокутників, трапецій, Симпсона. Оцінити похибку формули чисельного інтегрування двома способами: використовуючи теоретичну оцінку похибки та правило Рунге.

23 З яким кроком інтегрування потрібно обчислювати наближене значення інтеграла 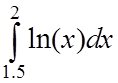 за формулою трапецій для того, щоб забезпечити точність 0.00001.