Розробка методичних вказівок до практичних занять з дисципліни «Обчислювальна геометрія та комп’ютерна графіка» за темою: "Візуалізація та анімація", страница 5

Переконайтеся в тому, що ключові кадри 0 і 20 не виділені. Якщо вони все ж виділені , то це виділення можна скасувати, утримуючи клавішу <Alt> і клацаючи на потрібних ключових кадрах.

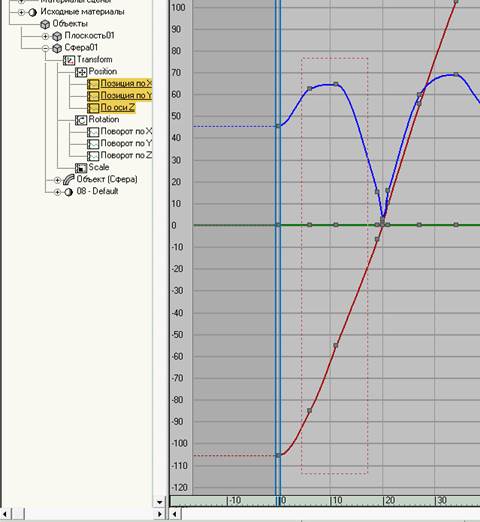
мал. 6.4.2. Вибір ключових кадрів, розташованих між
кадрами 0 і 20

6. Натисніть клавішу <Delete> для видалення виділених ключових кадрів.

7. Виділіть ключові кадри в проміжку від 20 до 40, за винятком кадрів 20 і 40, і
натисніть клавішу <Delete> для видалення виділених ключових кадрів. Тепер функціональні криві у вікні редактора матимуть такий вигляд, як на мал. 6.4.3.

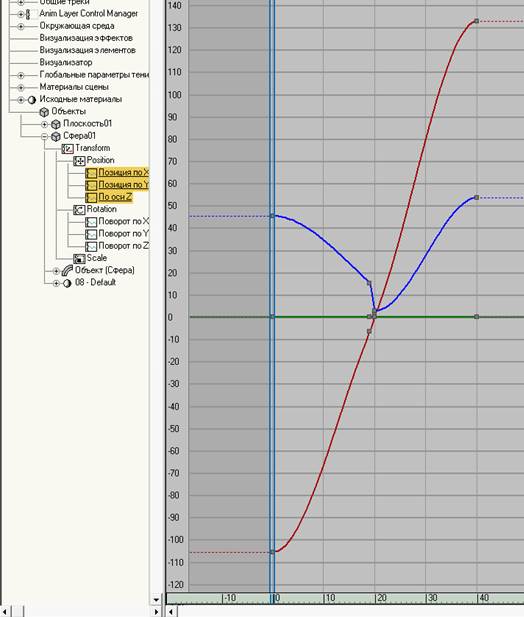
мал. 6.4.3. Функціональні криві переміщення після видалення деяких ключових кадрів.

Зміна типу інтерполяції

Мета даної вправи - створити природну імітацію відскоку м'яча. Якщо абсолютно пружний відскік м'ячика підпорядковується фізичним законам, то швидкість його руху уздовж осі X повинна залишатися постійною. Тому для функціональної кривої переміщення уздовж осі X потрібно використовувати тип інтерполяції Linear.

1. Виділіть трек X Position (Позиция по Х), клацнувши на його заголовку у вікні контролера, а потім виділіть ключовий кадр з номером 20 і видаліть його.

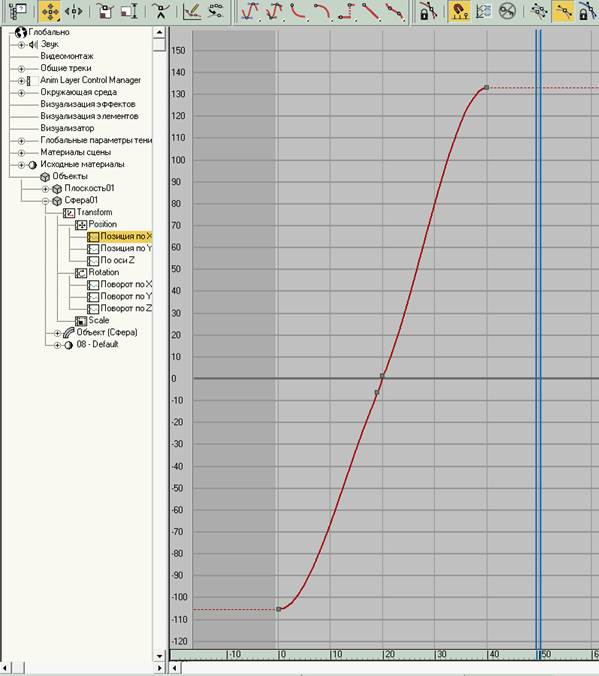
Мал. 6.4.4

2. Виділіть всі ключові кадри в проміжку від 0 до 40 і клацніть на кнопці Linear панелі Key Tangents у верхній частині діалогового вікна Track
View - Curve Editor (Просмотр треков-Редактор кривых). Тепер функціональна крива переміщення уздовж осі X буде прямою, що означає постійну швидкість переміщення (мал. 6.4.5).

У реальному світі швидкість м'ячика трохи зменшується після відскоку, але в даній вправі ця втрата кінетичної енергії не враховується.

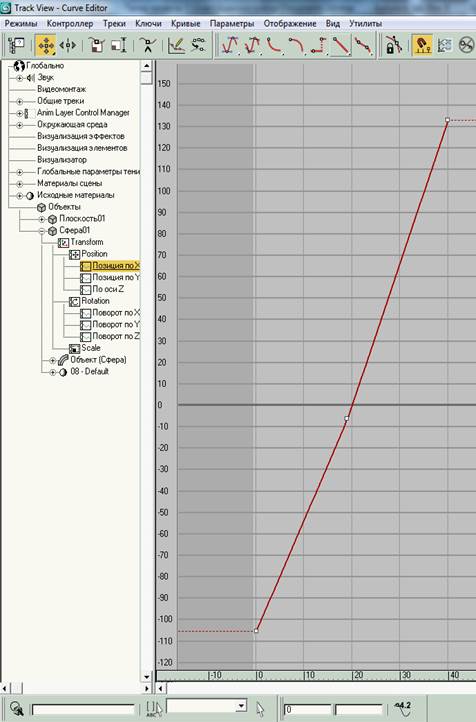
мал. 6.4.5. Лінійна інтерполяція функціональної кривої переміщення
уздовж осі X

Якщо обертання м'яча підпорядковується фізичним законам Ньютона, то він продовжить своє обертання в тому ж напрямку з постійною швидкістю.

3. Виділіть трек Y Rotation (Позиция по У), клацнувши на його заголовку у вікні контролера, а потім виділіть всі ключові кадри і вкажіть для функціональної кривої лінійний тип інтерполяції, клацнувши на кнопці Linear панелі Key Tangents у верхній частині діалогового вікна Track View - Curve Editor (просмотр треков-Редактор кривых). Тепер функціональна крива обернення навколо осі Y буде прямою лінією, що означає постійну швидкість обертання.

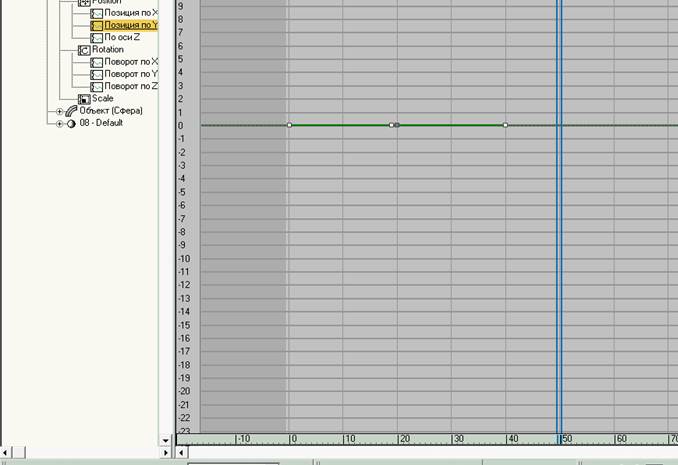
6.4.6

Редагування функціональної кривої Безьє

Прокрутіть отриманий анімаційний ролик до нульового кадру і запустіть його. Тепер м'ячик більш природно переміщується уздовж осі X і обертається навколо осі Y, але не відскакує.

1. У діалоговому вікні Track View - Curve Editor (просмотр треков-Редактор кривих) виділіть трек Z Position (По оси Z), клацнувши на
його заголовку у вікні контролера, а потім виділіть векторний маркер ключового
кадру з номером 0. Перетягніть векторний маркер вгору і вправо для редагування функціональної кривої, як показано на мал. 6.4.7.

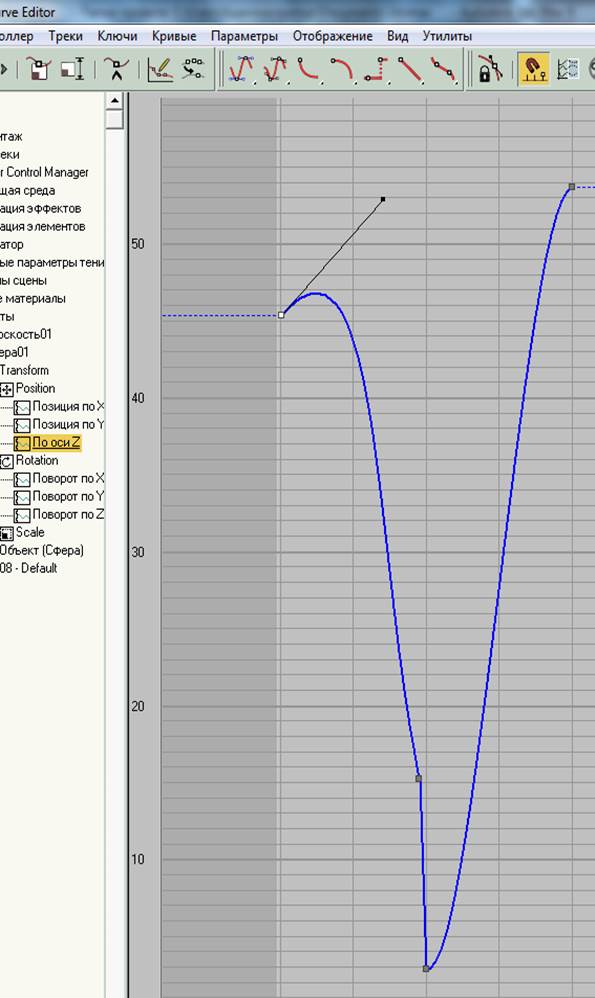
мал. 6.4.7. Редагування векторного маркера першого ключового кадру

2. Утримуючи натиснутою клавішу <Shift>, клацніть на одному з векторних маркерів ключового кадру з номером 20. Перетягніть його вгору, як показано на мал. 6.4.8, і відпустіть клавішу <Shift>. Тепер обидва векторних маркера розблоковані.

3. Клацніть на іншому векторному маркері ключового кадру з номером 20. Перетягніть його вгору, як показано на мал. 6.4.8, але тепер для цього вже не потрібно утримувати натиснутою клавішу <Shift>, так як векторні маркери стали незалежними.
4. Відредагуйте векторні маркери так; щоб функціональна крива нагадувала криву, показану на мал. 6.4.8. Прокрутіть отриманий анімаційний ролик до нульового кадру і налаштуйте функціональні криві. Для більш тонкого налаштування може знадобитися переміщення ключових кадрів з номерами 0 і 40.

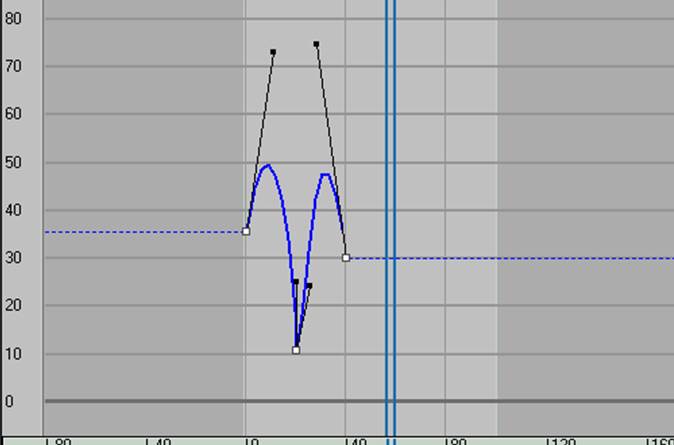
мал. 6.4.8. Функціональна крива треку Z Position (По оси Z)