Інтелектуальні системи
Практичне заняття №3
Тема: Генетичні алгоритми
Мета: отримати навички розв’язання практичних задач за допомогою генетичних алгоритмів.
Короткі теоретичні положення
Генетичні алгоритми (ГА) (Holland, 1969-1990) спрощено моделюють процеси природної еволюції і засновані на стохастических принципах. Генетичні алгоритми зводяться до виконання наступних етапів:
1. Ініціалізувати популяцію.
2. Обчислити значення критерію якості для кожної особини популяції.
3. Виконати процес відтворення для кожної особини популяції.
4. Виконати схрещування і мутацію для кожної особини популяції.
5. Повернутися до п. 2, якщо не виконано умову завершення.
Реалізація ГА зводиться до операцій з рядками: копіювання рядків, заміни фрагментів рядків і інверсії бітів. Розглянемо приклад.
Приклад.
Знайти
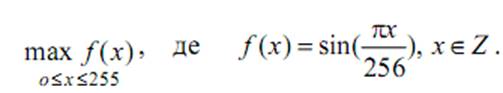
Функція залежить від однієї цілочисельної змінної. Особин популяції доцільно представити у вигляді бінарного рядка довжиною 1 байт.
|
Цілочисельне значення |
Двійкова хромосома |
|
0 |
00 00 00 00 |
|
1 |
00 00 00 01 |
|
… |
… |
|
255 |
11 11 11 11 |
Число особин популяції в реальних задачах зазвичай складає 10–100. У даній задачі виберемо 8.
1. Ініціалізація — за допомогою датчика випадкових чисел у кожній з 8 позицій кожного рядка встановимо або 0 або 1.
Результати ініціалізації наведено в табл. 3.1.
Таблиця 3.1. Ініціалізація початкової популяції
|
Особи |
x |
fx |
fnorm |
|
10111101 |
189 |
0.733 |
0.144 |
|
11011000 |
216 |
0.471 |
0.093 |
|
01100011 |
99 |
0.937 |
0.184 |
|
11101100 |
236 |
0.243 |
0.048 |
|
10101110 |
174 |
0.845 |
0.166 |
|
01001010 |
74 |
0.788 |
0.155 |
|
00100011 |
35 |
0.416 |
0.082 |
|
00110101 |
53 |
0.650 |
0.128 |
2. Значення критерію якості — нормоване значення функції
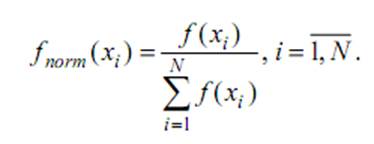
3. Формування нової популяції з тим же числом особин. При формуванні нової популяції використовується принцип рулетки (рис. 3.1). Результати застосування принципу рулетки показано в табл. 3.2.
Таблиця 3.2. Показники при формуванні покоління
за принципом рулетки
|
N |
Рядок |
Крит. якості |
% співвідн. |
|
1 |
01101 |
169 |
14.4 |
|
2 |
11000 |
576 |
49.2 |
|
3 |
10010 |
64 |
5.5 |
|
4 |
10011 |
361 |
30.9 |
|
Разом: |
1170 |
100 |
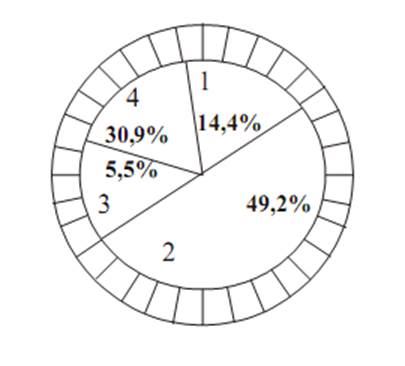
Рис. 5.1. Співвідношення за критерієм якості
Ймовірність влучення в кожний із сегментів пропорційна його величині. Генеруються N = 8 випадкових значень з діапазону [0,1]:
Якщо
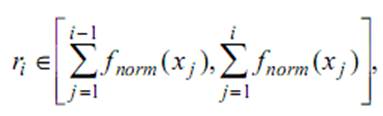
тоді
![]()
Наприклад,
якщо ![]() [0, 0.144], то в
нову популяцію включається
[0, 0.144], то в
нову популяцію включається ![]() .
Якщо
.
Якщо ![]() [0.144,
(0.144+0.093)=0.237], то
[0.144,
(0.144+0.093)=0.237], то ![]() включається
в нову популяцію.
включається
в нову популяцію.
Таким чином максимальна імовірність включення в нову популяцію особин з максимальним значенням критерію якості.
Візьмемо набір з 8 випадкових чисел:
0.293, 0.971, 0.160, 0.469, 0.664, 0.568, 0.371, 0.109.
Індекси особин першої популяції, що ввійдуть у наступне покоління:
3, 8, 2, 5, 6, 5, 3, 1.
Після відтворення популяція матиме вигляд:
01 10 00 11
00 11 01 01
11 01 10 00
10 10 11 10
01 00 10 10
10 10 11 10
01 10 00 11
10 11 11 01
4. Схрещування — основна риса генетичного алгоритму полягає в обміні частин двох батьківських особин.
a. Вибирається імовірність (приблизно 0.65–0.80) того, що між двома батьками відбудеться схрещування (виберемо Pc = 0.75).
b. Популяція випадковим образом розбивається на пари. Для будь-якої пари генерується випадкове число:
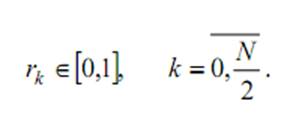
Якщо
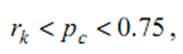
то пари піддаються схрещуванню.
c. Для кожної з пар, що підлягають схрещуванню, випадковим чином задаються два числа (або одне число для одноточкового схрещування), що визначають границі рядка для обміну (табл. 3.3).
Таблиця 3.3. Значення при схрещуванні
|
Батьківська популяція |
Нове покоління |
x |
f(x) |
|
01 110 002 11 |
01 11 01 11 |
119 |
0.999 |
|
00 111 012 01 |
00 10 00 01 |
33 |
0.394 |
|
… |
… |
… |
… |
|
111 01 120 00 |
10 10 10 00 |
168 |
0.882 |
|
110 10 121 10 |
11 01 11 10 |
222 |
0.405 |
|
… |
… |
… |
… |
|
012 00 10 110 |
10 00 10 10 |
138 |
0.998 |
|
102 10 11 110 |
01 10 11 10 |
110 |
0.976 |
|
… |
… |
… |
… |
|
01 10 00 11 |
01 10 00 11 |
99 |
0.937 |
|
10 11 11 01 |
10 11 11 01 |
189 |
0.733 |
|
Оптимальне значення |
10 00 00 00 |
128 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.