d. Мутація — інвертування випадково обраних бітів (зазвичай з постійною імовірністю для кожного біта популяції, приблизно рівною 0.001–0.01).
Таким чином будь-який біт інвертується з імовірністю 0.1%–1%. Оскільки в наведеному прикладі число бітів у популяції складає 64, то при імовірності мутації Pm =0.001 або 0.01 швидше за все жоден біт не змінить значення.
Тепер двом особинам нового покоління відповідає значення критерію якості >0.99.
5. Перехід до нової ітерації.
КОДУВАННЯ І ДЕКОДУВАННЯ ПАРАМЕТРІВ
|
Відповідність кодів |
||
|
Дес. |
Двійкові |
Грея |
|
0 |
0000 |
0000 |
|
1 |
0001 |
0001 |
|
2 |
0010 |
0011 |
|
3 |
0011 |
0010 |
|
4 |
0100 |
0110 |
|
5 |
0101 |
0111 |
|
6 |
0110 |
0101 |
|
7 |
0111 |
0100 |
|
8 |
1000 |
1100 |
|
9 |
1001 |
1101 |
|
10 |
1010 |
1111 |
|
11 |
1011 |
1110 |
|
12 |
1100 |
1010 |
|
13 |
1101 |
1011 |
|
14 |
1110 |
1001 |
|
15 |
1111 |
1000 |
Розрізняють кодування змінних параметрів, поданих цілими числами та числами з крапкою, що плаває.
Для кодування змінних, поданих цілими числами іноді використовують війкове подання змінної, при чому довжина хромосоми повинна бути достатньою для подання всіх можливих значень даної змінної. Але основним недоліком такого способу є те, що сусідні числа відрізняються в значеннях декількох бітів. (7(0111) і 8(1000)), що ускладнює функціонування ГА і збільшує час його збіжності. Щоб уникнути цього використовують код Грея. Його можна подати як двійковий з вагами розрядів gi=2i-1, тобто ... 15, 7, 3, 1.
При кодуванні декількох змінних необхідно провести кодування кожної у двійковий код, об’єднати отримані значення в один вектор і, розбиваючи його на тетради, перетворити за кодом Грея.
При кодуванні змінних, що подані числами з крапкою, що плаває застосовують таку послідовність:
- поділити весь інтервал припустимих значень змінної на ділянки з необхідною точністю;
- значення змінної визначають як номер інтервалу (ціле число), в середині якого знаходиться число.
Для коду Грея декодувальна функція має вигляд:
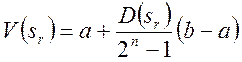
де aib– межі відрізка [a,b], що містять
значення змінної V, ![]() - десяткове подання
коду Грея.
- десяткове подання
коду Грея.
При кодуванні нечислових даних необхідно попередньо перетворити їх у числа.
Варіанти завдань
A. Для
знаходження максимуму функції f(x1, x2,
x3),
де xi Є[mini,
maxi] було
застосовано стандартних
генетичний алгоритм.
При формуванні хромосоми область визначення кожної змінної поділяли на 2n інтервали, значення змінної визначали як номер інтервалу (ціле число подане двійковим кодом). Після чого отримані значення об’єднували в один вектор, і розбиваючи його на тетради, перетворювали за кодом Грея.
Для двох хромосом С1, С2, сформованих випадковим чином, провести кросинговер, мутацію та інверсію. Серед нових представників популяції обчислити найбільш пристосованого.
1. f=(3-x1+x3)X2 x1Є[0, 1.5], x2Є[-0.7, 0.8] x2Є[0.5, 2], Δxi=0.1
Точка розриву при кросинговері знаходиться між 5 та 6 генами.
Операція мутації виконується для гена 1 та 3.
Операція інверсія виконується для частини хромосоми за 5 геном.
2. f=(3-x1*x3)X2 x1Є[1, 2.5], x2Є[-1, 0.5] x2Є[-1.5, 0], Δxi=0.1
Точка розриву при кросинговері знаходиться між 3 та 4 генами.
Операція мутації виконується для гена 2 та 3.
Операція інверсія виконується для частини хромосоми до 5 гена.
3. f=(10+x1+x3)X2*X3 x1Є[0, 1.5], x2Є[-1, 0.5] x2Є[0.5, 2], Δxi=0.1
Точка розриву при кросинговері знаходиться між 4 та 5 генами.
Операція мутації виконується для гена 5 та 6.
Операція інверсія виконується для частини хромосоми за 4 геном.
4. f=(x1+x3)X2*Х1 x1Є[0, 1.5], x2Є[-1.5, 0] x2Є[0.5, 2], Δxi=0.1
Точка розриву при кросинговері знаходиться між 2 та 3 генами.
Операція мутації виконується для гена 4 та 6.
Операція інверсія виконується для частини хромосоми до 4 гена.
5. f=(x2/(x3+x1))X2 x1Є[1, 2.5], x2Є[-0.7, 0.8] x2Є[0.5, 2], Δxi=0.1
Точка розриву при кросинговері знаходиться між 5 та 6 генами.
Операція мутації виконується для гена 1 та 5.
Операція інверсія виконується для частини хромосоми між 3 та 6 генами включно.
Б. Реалізуйте генетичний алгоритм для розв’язання задачі максимізації функції:
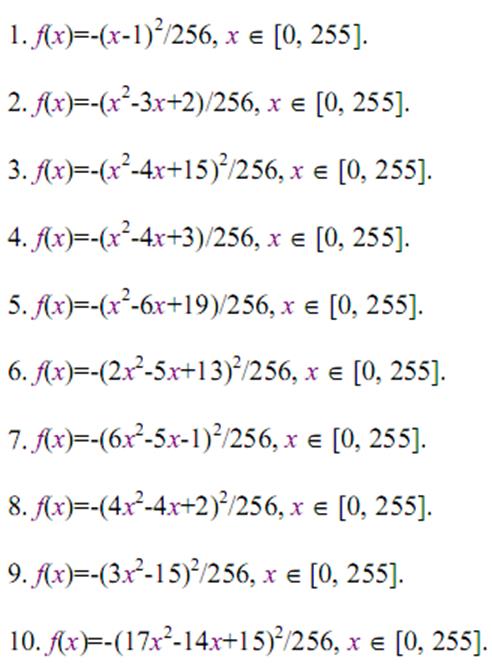
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.