Предмет, метод и задачи статистики. Статистическое наблюдение. Статистическая сводка и группировка. Средние величины и показатели вариации, страница 7

6.1  Понятие о рядах динамики и их виды, правила формирования

6.2  Основные показатели динамики и их определение

6.3  Выявление и изучение основной тенденции развития явлений

6.4  Статистическое изучение сезонных колебаний

Рядами динамики (РД) называются – статистические данные, характеризующие изменение явлений во времени.

Иначе говоря, РД – это перечень числовых значений какого-либо статистического показателя в последовательные моменты или периоды времени.

В соответствии с этим ряды динамики подразделяются на моментные и интервальные.

Основные задачи, решаемые посредством анализа РД:

1.  Характеристика среднего уровня и средней интенсивности изменения явлений во времени.

2.  Характеристика интенсивности изменения отдельных уровней изучаемых явлений во времени.

3.  Характеристика основной тенденции развития явлений.

4.  Характеристика сезонных колебаний в явлениях, связанных со сменой сезонов.

5.  Интерполяция, экстраполяция и прогнозирование развития явлений.

Для интервальных рядов с равными интервалами времени средний уровень ряда рассчитывается по формуле средне арифметической простой:

,

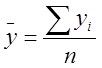где Sy_i – сумма уровней ряда;

n – число уровней.

Если интервалы времени неравные – применяется средняя арифметическая взвешенная:

 ,

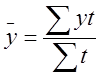где t – длительность отдельных промежутков времени (т.е. число дней, месяцев, лет) в каждом из интервалов.

Для моментных рядов с равноотстоящими уровнями средний уровень рассчитывается по формуле средней хронологической:

 ,

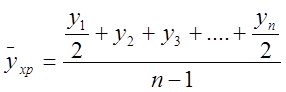где y₁ –  начальный уровень ряда;

y_n – конечный уровень ряда;

n – число уровней.

РД характеризуются специфическими показателями, показывающими характер динамики и изменение уровней во времени.

Такими показателями являются:

1)  – абсолютный прирост;

2)  –  коэффициент (темп) роста;

3)  – темп прироста;

4)  – абсолютное значение 1% прироста.

Абсолютный прирост – рассчитывается как разность между двумя уровнями ряда:

  – цепной;

– базисный.

Он показывает, на сколько единиц в абсолютном выражении уровень одного периода больше или меньше предыдущего уровня.

Следовательно, может быть как со знаком (+), так и (-).

( Со знаком (-) – абсолютное снижение).

Надо сказать, что абсолютный прирост может быть и относительной величиной, если ряд состоит из относительных величин.

Коэффициент роста –  относительный показатель, характеризующий отношение данного уровня к уровню, принятому за базу сравнения.

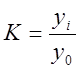– базисны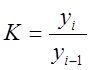й;    – цепной.

Он показывает, во сколько раз уровень данного периода больше или меньше базисного уровня.

Коэффициент роста, выраженный в %-тах, называется темпом роста.

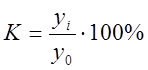– базисны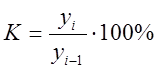й;      – цепной.

Темп прироста характеризует абсолютный прирост в относительных величинах – относительный показатель, показывающий, на сколько процентов один уровень больше (или меньше) базисного уровня.

Чаще его рассчитывают путем вычитания 100 % из темпа роста:

,         .

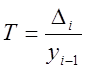
Абсолютное значение 1 % прироста = сотой части предыдущего уровня:

,           .

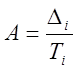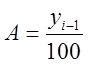Приведенные показатели являются одними из основных показателей, используемых при анализе рядов динамики. Кроме того, для всех перечисленных выше показателей могут быть рассчитаны их обобщающие показатели в виде средних величин:

–  среднегодовой абсолютный прирост;

–  среднегодовой коэффициент роста;

–  среднегодовой темп роста;

–  среднегодовой темп прироста.

Среднегодовой абсолютный прирост рассчитывается как средняя арифметическая из абсолютных приростов за (n) лет, т.е.:

.

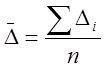Или

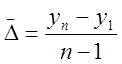 – на основе данных об абсолютном приросте за весь рассматриваемый период.

Среднегодовой коэффициент (или темп) роста рассчитывается как средняя геометрическая из годовых коэффициентов роста, рассчитанных по отношению к предыдущему периоду:

.

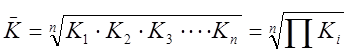Если данные о коэффициентах роста по отдельным годам отсутствуют, то средний годовой темп роста можно рассчитать по формуле:

,

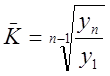где у_n – конечный уровень ряда,

       у₁ – начальный уровень ряда,

       n – число уровней.