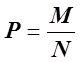 , где
, где ![]() – число
единиц, обладающих данным признаком. Может быть выражена в долях единицы или в
%-тах (относительная величина);
– число
единиц, обладающих данным признаком. Может быть выражена в долях единицы или в
%-тах (относительная величина);
![]() – генеральная дисперсия;
– генеральная дисперсия;
![]() – генеральное СКО.
– генеральное СКО.
Аналогичные показатели выборочной совокупности называются выборочными и обозначаются:
![]() – выборочная совокупность (часть единиц
генеральной совокупности, попавшая в выборку);
– выборочная совокупность (часть единиц
генеральной совокупности, попавшая в выборку);
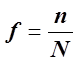 – доля отбора, часть единиц генеральной
совокупности, попавшая в выборку;
– доля отбора, часть единиц генеральной
совокупности, попавшая в выборку;
![]() – выборочная средняя (средняя величина
какого-либо признака в выборочной совокупности);
– выборочная средняя (средняя величина
какого-либо признака в выборочной совокупности);
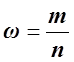 – выборочная доля, где
– выборочная доля, где ![]() – доля единиц выборки, обладающих данным
признаком.
– доля единиц выборки, обладающих данным
признаком.
![]() – выборочная дисперсия;
– выборочная дисперсия; 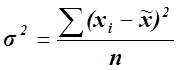 ;
;
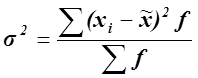 ;
;
![]() – виборочное СКО.
– виборочное СКО.
Ошибки выборки и теоретические основы выборочного метода.
Обычно составляют такие показатели выборочной и генеральной совокупности:
– среднюю величину того или иного признака у единиц совокупности (ср.зарплата, ср. доход, ср. урожайность);
– долю единиц, обладающих тем или иным признаком, т.е. удельный вес определенных единиц в совокупности (доля лиц с высшим образованием, доля женщин в общей численности работников и т.д.).
Разность между этими показателями выборочной и генеральной совокупности и называется ошибкой репрезентативности, т.е.:
![]() ,
ошибка репрезентативности средней,
,
ошибка репрезентативности средней,
![]() , ошибка репрезентативности для доли.
, ошибка репрезентативности для доли.
1. При повторном собственно-случайном отборе:
–
для средней величины признака: 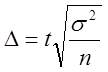 ;
;
–
для доли: 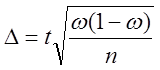 .
.
2. При бесповторном собственно-случайном и механическом:
–
для средней: 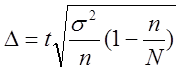 ;
;
–
для доли: 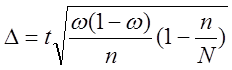 .
.
3. При типическом отборе дисперсией признака является средняя из внутригрупповых дисперсий:
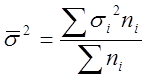 ,
,
где
![]() – виборочная дисперсия в i-той
типической группе, она определяется по формуле:
– виборочная дисперсия в i-той
типической группе, она определяется по формуле: 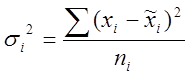 ;
;
![]() – число
единиц в i-ой типической группе.
– число
единиц в i-ой типической группе.
Для доли средняя из внутригрупповых дисперсий определяется:
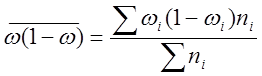 .
.
Тогда предельная ошибка выборочной средней при типическом повторном отборе будет равна:
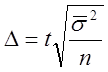 ;
;
доли: 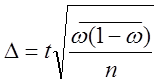 .
.
4. При типическом бесповторном отборе:
для средней: 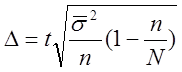 ;
;
для доли: 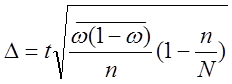 .
.
Предельная ошибка выборки при типическом отборе всегда меньше ошибки при собственно-случайном отборе, так как групповая дисперсия меньше общей дисперсии.
5. При серийном (гнездовом) отборе каждая из отобранных серий рассматривается как единица совокупности.
Мерой колеблемости
является межсерийная выборочная дисперсия (![]() ), т.е.
средний квадрат отклонений серийных выборочных средних от общей выборочной
средней:
), т.е.
средний квадрат отклонений серийных выборочных средних от общей выборочной
средней:
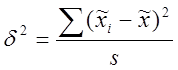 ,
,
где ![]() – средняя по каждой серии;
– средняя по каждой серии;
![]() – общая выборочная средняя;
– общая выборочная средняя;
![]() – число отобранных серий.
– число отобранных серий.
Предельная
ошибка средней при серийном повторном отборе: 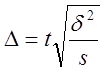 ;
;
ошибка
доли: 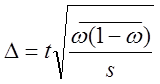 .
.
6. При серийном бесповторном отборе:
для средней: 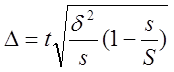 ;
;
для доли: 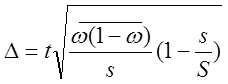 ,
,
где ![]() – межсерийная дисперсия;
– межсерийная дисперсия;
![]() – число отобранных
серий (в выборочной совокупности);
– число отобранных
серий (в выборочной совокупности);
![]() – число серий в
генеральной совокупности.
– число серий в
генеральной совокупности.
Определение необходимой численности выборки
Таблица 8.1 – Предельные ошибки выборки
|
отбора Виды Выборок |
Повторный |
Бесповторный |
|||
|
для средней |
Для Доли |
для средней |
для доли |
||
|
Собственно-случайный и механи-ческий |
|
|
|
|
|
|
Типический |
|
|
|
|
|
|
Серийный |
|
|
|
|
|
ТЕМА 10. ГРАФИЧЕСКИЙ СПОСОБ ИЗОБРАЖЕНИЯ СТАТИСТИЧЕСКИХ ДАННЫХ
9.1 Роль, сущность и назначение статистических графиков, основные требования к ним
9.2 Элементы графиков и правила их построения, виды графиков
9.3 Диаграммы и особенности их построения
9.4 Линейные графики, картограммы и кардиограммы
Статистический график представляет собой условное изображение статистических величин посредством линий, геометрических фигур, рисунков или схематических географических карт.
Главная задача графиков – наглядное представление фактов социально-экономической жизни.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.