Чем сильнее связь между признаками, тем теснее будут располагаться точки корреляционного поля вокруг определенной линии, выражающей форму связи (рис. 1).
Основные понятия и задачи корреляционного анализа
Корреляционный анализ – метод математической статистики, изучающий корреляционные (статистические) связи.
В статистике различают следующие варианты корреляционных связей.
1. Парная корреляция, т.е. зависимость между двумя признаками – результатным и факторным (или двумя факторными).
2. Частная корреляция – зависимость между результатным и одним из факторных признаков при фиксированном значении других факторных.
3. Множественная корреляция – зависимость между результатным и двумя и более факторными признаками.
Необходимо отметить, что при изучении корреляционных связей статистика, наряду с корреляционным, использует и регрессионный анализ. Поэтому корректней было бы сказать о применении методов КРА в изучении корреляционных связей, но для краткости говорят просто – корреляционный анализ.
Наиболее сложным и ответственным этапом КРА является подбор уравнения, характеризующего сущность связи. При парной корреляции уравнение связи может быть установлено при помощи построения корреляционного поля, составления корреляционных таблиц, пересмотра различных функций.
– линейная форма уравнением прямой линии:
![]() ;
;
– нелинейная форма уравнениями различного рода кривых линий:
· параболы 2-го порядка ![]() или высших порядков,
или высших порядков,
· гиперболы 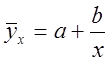 ,
,
· показательной функции ![]() и др.
и др.
Подобранное уравнение называется уравнением регрессии или корреляционным уравнением. Его основная задача – установление количественной взаимосвязи между признаками.
Неизвестные параметры уравнения ![]() и
и ![]() определяют
способом наименьших квадратов из системы нормальных уравнений.
определяют
способом наименьших квадратов из системы нормальных уравнений.
![]() .
.
Система нормальных уравнений для парной линейной связи имеет вид:
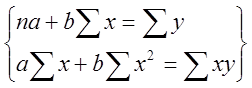 ,
,
де ![]() – количество элементов
факторного признака
– количество элементов
факторного признака ![]() .
.
Параметры ![]() и
и ![]() искомой прямой можно определить и
по другим формулам:
искомой прямой можно определить и
по другим формулам:
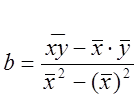 ,
, ![]() .
.
Оценка тесноты связи между признаками предполагает определение меры соответствия вариации результатного признака и факторного (или нескольких факторных при множественной корреляции).
В случае линейной зависимости тесноту связи можно измерить при помощи линейного коэффициента корреляции:
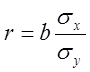 ,
,
где ![]() – коэффициент регрессии;
– коэффициент регрессии;
![]() – среднее
квадратическое отклонение факторного признака;
– среднее
квадратическое отклонение факторного признака;
![]() – среднее
квадратическое отклонение результатного признака;
– среднее
квадратическое отклонение результатного признака;
![]() ;
; ![]() .
.
Линейный коэффициент корреляции можно определить и по иной формуле:
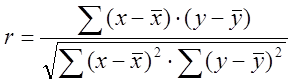 или
или 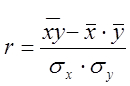 .
.
Линейный коэффициент корреляции может принимать значения от 0 ± 1 (знак (+) при прямой зависимости, (-) при обратной).
На практике руководствуются следующими оценками тесноты связи:
При ![]() < 0,3 – связь слабая;
< 0,3 – связь слабая;
![]() = 0,3 ¸ 0,7 – средняя;
= 0,3 ¸ 0,7 – средняя;
![]() > 0,7 – сильная;
> 0,7 – сильная;
![]() =
0 – связь отсутствует;
=
0 – связь отсутствует;
![]() =
1 – связь функциональная.
=
1 – связь функциональная.
Значимость ЛКК проверяется на достоверность (надежность). Считается, что корреляционная связь является достоверной лишь при достаточном числе наблюдений (не менее 20 – 30). Проверка надежности коэффициента корреляции осуществляется с помощью критерия надежности по формуле:
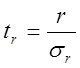 ,
,
где ![]() – среднеквадратическая
ошибка коэффициента корреляции:
– среднеквадратическая
ошибка коэффициента корреляции: 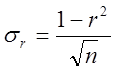 ,
,
где ![]() – число наблюдений.
– число наблюдений.
Если ![]() ³ 3, то
³ 3, то ![]() считается надежным, а связь
доказанной с вероятностью 0,997.
считается надежным, а связь
доказанной с вероятностью 0,997.
Если ![]() < 3, связь нельзя
считать достоверной.
< 3, связь нельзя
считать достоверной.
Из формулы средней квадратической ошибки видно, что эта ошибка находится в обратной зависимости от числа наблюдений.
Для всех иных форм связи теснота ее может быть определена с помощью теоретического корреляционного отношения:
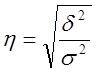 ,
,
где 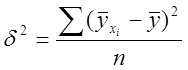 – дисперсия выравненных
значений результатного признака (
– дисперсия выравненных
значений результатного признака (![]() );
);
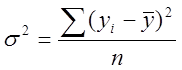 – дисперсия фактических
значений результатного признака (
– дисперсия фактических
значений результатного признака (![]() ).
).
Если ![]() , значит
, значит ![]() и вариация
и вариация ![]() полностью
зависит от вариации
полностью
зависит от вариации ![]() .
.
Если ![]() , значит вариация
, значит вариация ![]() никак не влияет на вариацию
никак не влияет на вариацию ![]() и в этом случае
и в этом случае ![]() .
То есть, чем ближе
.
То есть, чем ближе ![]() к 1, тем связь теснее, а чем
ближе к нулю, тем слабее.
к 1, тем связь теснее, а чем
ближе к нулю, тем слабее.
ТЕМА 7. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ ДИНАМИКИ СОЦИАЛЬНО–ЭКОНОМИЧЕСКИХ ЯВЛЕНИЙ И ПРОЦЕССОВ
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.