где ![]() – число групп.
– число групп.
3. Построить шкалу интервалов. Т.е. построить первую колонку ряда, показывающую границы интервалов. При этом необходимо указать на обозначение границ интервалов.
На практике часто случается так, что верхняя граница одного интервала совпадает с нижней границей последующего. При этом неясно в какую группу должны быть отнесены единицы совокупности, числовые значения признака у которых совпадают с одной из границ.
Так как статистика изучает массовые явления и процессы, то статистический показатель – это обобщающая характеристика какого-либо свойства совокупности в целом или ее отдельной части (группы).
Абсолютные величины – это статистические показатели, характеризующие либо суммарное число единиц совокупности (объекта), либо ее суммарное свойство – размер, объем, вес, уровень.
Относительные величины – это статистические показатели, характеризующие количественное соотношение двух сопоставимых статистических показателей. Иначе говоря, это результат соотношения двух статистических показателей.
Виды относительных величин.
По характеру, назначению и сущности выражаемых соотношений различают следующие виды относительных величин: структуры, динамики, интенсивности, координации, сравнения, выполнения плана (нормы), планового задания.
ТЕМА 5. СРЕДНИЕ ВЕЛИЧИНЫ И ПОКАЗАТЕЛИ ВАРИАЦИИ
4.1 Сущность значение средних величин
4.2 Виды средних и способы их расчета
4.3 Порядковые средние (медиана и мода)
4.4 Показатели вариации и их расчет
Средней величиной в статистике называется показатель, характеризующий обобщенное значение варьирующего признака единиц совокупности.
Главное значение средних величин состоит в их обобщающей функции, т.е. в замене множества различных индивидуальных значений признака их средней величиной, характеризующей всю совокупность.
Средняя арифметическая простая применяется в тех случаях, когда каждое индивидуальное значение признака (числовой вариант) встречается один раз или одинаковое число раз.
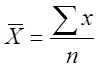 .
.
Средняя арифметическая взвешенная применяется в тех случаях, когда значения признака в совокупности встречаются много раз и неодинаковое число раз. Т.е. когда варианты варьирующего признака имеют различные частоты. В подобных случаях мы имеем дело, как нам уже известно, со сруппированными данными или с вариационными радами распределения.
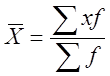 .
.
![]() ,
,
где
![]() – произведение
– произведение ![]() .
.
Средняя гармоническая обычно применяется в случаях, когда осреднению
подлежат не сами варианты, а обратные им числа  или
когда есть данные об общем объеме явления и индивидуальных значениях признака,
но нет сведений о количестве единиц данного явления (частотах).
или
когда есть данные об общем объеме явления и индивидуальных значениях признака,
но нет сведений о количестве единиц данного явления (частотах).
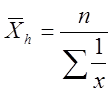 .
.
Средняя квадратическая применяется в случаях, когда осреднению (обобщению) подлежат величины, выраженные в виде квадратных функций.
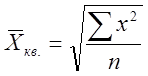 .
.
Взвешенная: 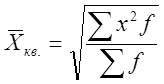 .
.
Медиана – значение варьирующего признака, расположенного в середине ранжированной совокупности и разделяющее совокупность на две равные части – со значениями признака меньше и больше медианы.
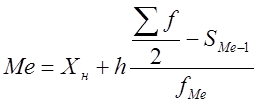 ,
,
где ![]() – нижняя граница
медианного интервала;
– нижняя граница
медианного интервала;
![]() –
величина медианного интервала;
–
величина медианного интервала;
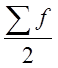 –
порядковый номер Ме ;
–
порядковый номер Ме ;
![]() –
накопленная частота до медианного интервала;
–
накопленная частота до медианного интервала;
![]() –
частота медианного интервала.
–
частота медианного интервала.
В статистике модой (Мо) называется такое значение варьирующего признака, которое наиболее часто встречается у единиц данной совокупности.
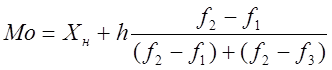 ,
,
где ![]() – нижняя граница
модального интервала;
– нижняя граница
модального интервала;
![]() –
величина модального интервала;
–
величина модального интервала;
![]() – частота предмодального
интервала;
– частота предмодального
интервала;
![]() – частота модального
интервала;
– частота модального
интервала;
![]() – частота
послемодального интервала.
– частота
послемодального интервала.
Вариацией, т.е. колебанием, изменением признака называется различие его значений у разных единиц совокупности в один и тот же момент или период времени.
Показателями вариации в статистике являются:
1. Вариационный размах (амплитуда колебаний).
2. Среднее линейное отклонение.
3. Средний квадрат отклонений (дисперсия).
4. Среднее квадратическое отклонение (стандартное отклонение).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.