Математика \ Статистика

Предмет, метод и задачи статистики. Статистическое наблюдение. Статистическая сводка и группировка. Средние величины и показатели вариации, страница 5

5. Коэффициент вариации.

Вариационный размах

где – размах вариации,

– наибольшее значение признака,

– наименьшее значение признака.

Среднее линейное отклонение .

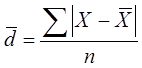где – среднее линейное отклонение;

– конкретное значение варианта признака;

– среднее значение признака;

– число вариантов.

Дисперсия представляет собой среднюю величину из квадратов отклонений отдельных значений признака от их средней арифметической.

простая ;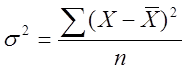

взвешенная .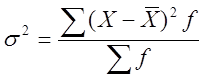

Средне квадратическое отклонение представляет собой корень квадратный из дисперсии.

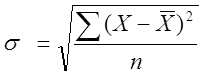Взвешенное: .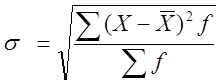

ТЕМА 6. СТАТИСТИЧЕСКОЕ ИЗУЧЕНИЕ СВЯЗИ МЕЖДУ ЯВЛЕНИЯМИ

5.1 Взаимосвязи общественных явлений и необходимость их статистического изучения

5.2 Виды и формы взаимосвязи между явлениями

5.3 Основные приемы и методы изучения взаимосвязей

5.4 Понятие о корреляционно-регрессионном анализе

5.5 Теснота связи и простейшие методы ее измерения

Между причиной и следствием часто существует взаимодействие. То есть следствие может, в свою очередь, оказывать влияние на причину.

По характеру зависимости между факторными и результатными признаками связи подразделяются на:

– функциональные или строго детерминированнные (от латинского determinatio – ограничение, определение), т.е. строгие, полные;

– стохастические, т.е. вероятностные, нестрогие.

Стохастические – это связи, при которых каждому значению факторного признака соответствует множество значений результатного признака, которые варьируют и не имеют строго определенной зависимости от изменения величины факторного признака.

Частным случаем стохастических связей являются корреляционные (статистические). Это связи, при которых каждому значению факторного признака соответствует среднее значение результатного признака .

Корреляционные связи по направлению бывают прямыми и обратными.

По аналитическому выражению корреляционные связи подразделяются на прямолинейные (линейные) и нелинейные (криволинейные).

Корреляционные связи могут быть также различной степени тесноты. Если значению факторного признака соответствуют близкие друг другу (тесно расположенные около своей средней) значения результатного признака – связь является тесной.

Для выявления наличия связи, ее формы и направления в статистике используются различные методы:

– метод сопоставления параллельных рядов;

– графический;

– аналитических группировок;

– корреляционно-регрессионного анализа (КРА).

Графический метод – позволяет выявить наличие связи двух признаков при помощи построения и анализа поля корреляции.

Для этого в системе координат на оси абсцисс откладываются значения факторного признака, а на оси ординат – результатного. Получим некоторое рассеивание множества точек – так называемое корреляционное поле.

По расположению точек в корреляционном поле можно сделать вывод о наличии связи, ее направлении и тесноте.