Основні проблеми чисельного розв’язання задач. Класифікація похибок, страница 8

  Більшість задач чисельного аналізу в загальному вигляді можна записати у вигляді рівняння

 y=F(x),                              (1.11)

де F:XàY ¾ деякий оператор, що задає відображення метричного простору Х у метричний простір У( дивись Додаток 1.1).

  Загальний підхід, що реалізується в наближених методах розв’язання таких задач, полягає в заміні рівняння (1.11) близьким йому, простішим (як правило, скінченновимірним) рівнянням                                     

у_n=F_n(x_n) .                            (1.12)

  Тут F_n:X_nàY_n – оператор, що відповідає вихідному оператору F. При цьому елементи x_n є X_n та y_n є Y_n розглядаються як образи елементів x є X та y є Y. Цей роз’язок можна визначити через відповідні оператори

  x_n=j(x), y_n=y(y)   .                     (1.13)

Як відомо, заміна одних математичних об’єктів іншими, чимось близькими до них, називається апроксимацією.

Визначення 1 Рівняння

 F_n(x_n)=yn(y)                          (1.14)

апроксимує рівняння 1.11 (оператор F_n апроксимує F), якщо для будь-яких елементів х з D(F)ÍX  міра апроксимації

 r_yn(F_n(j_n(x)),y_n(F(x)))® 0 , коли  nൠ.    (1.15)

(Тут r_yn(a,b)) визначає метрику, тобто відстань між елементами a,bÎY_n ).

  Щоб можна було порівнювати якість різних моделей вигляду (1.14) для задачі (1.11), користуються поняттям порядку апроксимації. Ця характеристика пов’язує прямування до 0 міри апроксимації (1.15) з порядком зменшення деякої залежної від n малої величини, наприклад, кроку апроксимації.

  Будемо вважати, що розв’язки  х*ÎХ, та  рівнянь відповідно (1.11) та (1.14) існують і єдині. Наближеним розв’язком задачі (1.11) вважається елемент , де  обернене до  відображення .

  Головним питанням будь-якої теорії наближених методів розв’язання задач вигляду (1.11) є питання про те, чи можна  наближеним розв’язком х⁽ⁿ⁾ як завгодно добре відобразити поведінку точного розв’язку х*. Це питання про збіжність х⁽ⁿ⁾ до х*.

Визначення 2 Має місце збіжність наближеного розв’язку х⁽ⁿ⁾ до точного розв’язку х* рівняння (1.11), якщо

                          .

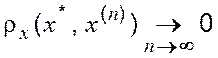  Наявність фактичних оцінок величин  дозволяє не тільки робити висновки про збіжність наближених розв’язків, але і визначати похибки отриманих наближень до розв’язку.

  Питання про збіжність розв’язків у⁽ⁿ) до у* тісно пов’язане з тим, чи можна надійно розв’язати спрощену задачу (1.14). Адже спрощена задача також розв’язується наближено. Покращання якості апроксимації  шляхом зменшення її міри (1.15) спричинює збільшення розмірності n для задачі (1.14), а отже, збільшення об’єму обчислень, що може призвести до збільшення обчислювальних похибок .

Визначення 3 Обчислювальний процес називається стійким, якщо малі похибки вхідних даних викликають малі похибки результатів.

 Питання і завдання до розділу 1

1  Джерела й класифікація похибок. Наближені числа.  Абсолютна й відносна похибки. Правильні й значущі цифри. Способи округлення.

2  Подання чисел в ЕОМ. Машинний нуль, машинна нескінченність, машинний іпсилон. Алгоритми обчислення.

3  Похибки арифметичних операцій над наближеними числами.

4  Похибки обчислення функцій однієї та декількох змінних.

5   Похибки обчислення неявно заданої функції.

6 Числа  задані наближено:
,, Відомо, що ,,. Записати ці числа з усіма правильними знаками.

7  Наближене число a містить 5 правильних цифр. Що можна сказати про відносну похибку числа a?

8  З якою відносною похибкою потрібно знайти наближене значення числа a, щоб правильними виявилися 5 значущих цифр?

9  Для наближених чисел a та b (a>b>0) відомо, що (a)=(b)=. Оцінити похибки:
 а)  (a+b),  b) ,(a-b), c) (a*b), d) (a/b).

10  Числа a та b задані наближено: , , . Оцінити похибки:
 a)різниці , b) добутку .
Записати відповідь з урахуванням  правильних цифр.

11 Визначити правила оцінки абсолютних і відносних   похибок функцій

 a);  b)  c) .

12  Функція 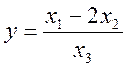  обчислюється при значеннях , , . Знайти значення  . Записати результат з усіма правильними цифрами.

13  Коефіцієнти  обчислюються з відносною похибкою (a)=(b)=(с)=. Знайти максимальну похибку, з якою можуть обчислюватися корені рівнянь:  a) ; b) .

14  Функція 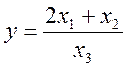 обчислюється при значеннях , ,. Визначити  при яких значеннях   відповідь буде містити 3 правильні цифри.