Основні проблеми чисельного розв’язання задач. Класифікація похибок, страница 7

Погано обумовлені задачі є з погляду обчислювача великою проблемою. У таких задачах неминучі помилки округлення й похибки у вхідних даних катастрофічно наростають, роблячи одержувану відповідь неприйнятною. Погано обумовлені задачі становлять небезпеку при отриманні числового розв’язку. Потрібно вміти виявляти погану обумовленість і боротися з нею.

Відмінна риса погано обумовлених задач така: мале відхилення у вхідних даних призводить до суттєвих змін відповіді. Якщо розглядати результат обчислень як функцію y(x) від вхідних даних, то мале відхилення dx аргумента приведе до зміни обчисленого значення на dy, причому |dy| можна оцінити як добуток модуля похідної та абсолютної величини відхилення: . У випадку поганої обумовленості малі зміни аргументу (вхідних даних) приводять до суттєвих змін у відповіді, тобто похідна  набуває більших за модулем значень. Як правило, працюють із відносними приростами

Dx = dx/x, Dy = dy/y.

У цьому випадку . Число  називається числом обумовленості задачі. Отже,

 або .

Якщо помилки у вихідних даних обумовлені винятково використанням машинної арифметики, то , де  – точність машинної арифметики. Машинним іпсилоном  називається мінімальне додатне число, що при додаванні до числа 1.0 дає результат, більший ніж 1.0. Величина машинного іпсилона визначає відносну похибку введених чисел і, таким чином, є найважливішою характеристикою машинної арифметики. У цьому випадку  і . Таким чином, чим більше число обумовленості, тим сильніший вплив похибки вхідних даних і похибки, внесеної округленнями.

Іноді дуже прості задачі демонструють погану обумовленість.

Приклад. Розглянемо задачу знаходження кореня многочлена

f(t)=(t-2)⁹=t⁹–18t⁸+144t⁷–672t⁶+2016t⁵–4032t⁴+5376t³–4608t²+2304t–512.

Якщо многочлен заданий за допомогою першої з наведених формул, то задача знаходження кореня не становить проблеми. Нехай многочлен заданий за допомогою іншої формули, тобто задані його коефіцієнти й відомо, що один із коренів локалізований на відрізку [1,3]. Тоді значення многочлена можна обчислювати за схемою Горнера

f(t) = ((((((((t – 18)t + 144)t – 672)t + 2016)t –4032)t + +5376)t – 4608)t + 2304)t – 512,

а корінь можна знайти за методом дихотомії. Розглянемо поведінку функції на відрізку [1.97,2.03]. Обчислення виконувалися з подвійною точністю (double). Значення функції обчислювалися із кроком 0.0001. На першому малюнку показані результати при обчисленні за першою з наведених формул, а на другому – при обчисленні за схемою Горнера.

                               Рис. -1.1

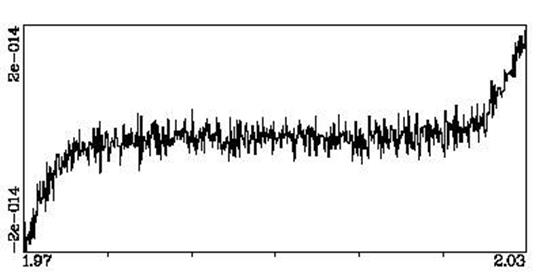
                                   Рис. -1.2

Бачимо, що в околі точки t=2 функція, обчислена за схемою Горнера, поводиться непередбачувано. Якщо ми спробуємо знайти чисельно корінь рівняння f(t) = 0 для функції f(t), що обчислюється за схемою Горнера, то одержимо випадкову точку з відрізка [1.98, 2.02]. На цьому відрізку зміна функції становить менш ніж 4e-14, але відрізок невизначеності для кореня виходить великий – довжиною 0.04.

Обмежимося простим і нестрогим зауваженням, що з’ясовує природу поганої обумовленості цієї задачі. Якщо точка t пробігає діапазон [2-e,2+e] при деякому досить малому значенні e (наприклад, при e<0.01), то значення функції f(t) змінюється дуже мало. Відповідно, мала зміна функції f(t) (або коефіцієнтів многочлена) приведе до великої зміни значення кореня.

1.10 Прості тести на обумовленість

У погано обумовленій задачі відповідь дуже залежить від будь-яких похибок як у вхідних даних, так і внесених у процесі обчислень. Це дозволяє використовувати наступні прості тести на погану обумовленість.

· Можна спробувати змінити вхідні дані, вносячи в них малі випадкові помилки. У випадку поганої обумовленості відповідь повинна при цьому суттєво змінюватися.

· Можна спробувати повторити розрахунок з використанням машинної арифметики різної точності. Саме із цього погляду корисно визначати свій дійсний тип так, щоб зміна точності арифметики зводилася просто до перекомпіляції. Сильна залежність відповіді від точності використовуваної арифметики свідчить про слабку обумовленість.

· Можна внести штучну похибку у деякі із проміжних результатів. Для цього можна просто округляти обчислені значення до заданої кількості значущих цифр.

1.11 Загальна схема розв’язання задач чисельного аналізу. Апроксимація, стійкість, збіжність