Основні проблеми чисельного розв’язання задач. Класифікація похибок, страница 5

Розглянемо віднімання двох майже рівних чисел. Запишемо вираз для відносної похибки різниці у вигляді

При ця похибка може бути як завгодно великою. Нехай а1=2520, а2=2518. Абсолютні похибки вихідних даних а1=а2=0.5; відносні похибки - а1а20.002 (0.2%). Відносна похибку різниці буде дорівнювати (а1-а2)=(0.5+0.5)/2=0.5 (50%). Оскільки в подальших обчисленнях ця велика відносна похибка буде поширюватися, може виявитися сумнівною точність остаточного результату обчислень.

Наведемо деякі оцінки

Дія (функц.)

Абсолютна похибка

Відносна похибка

х1+х2

х1-х2

x1*x2

x1/x2

a₁+a₂

У той же час буває і так, що похибки чисел, що беруть участь у тому або іншому обчисленні, взаємно компенсуються. Врахувати це можливо, але досить складно. Для ознайомлення з різними питаннями наближених обчислень можна порекомендувати книги [1],[2].

1.5 Підвищення точності результатів обчислень (рекомендації)

Щоб зменшити можливу похибку результату при розв’язуванні задачі, рекомендується дотримуватися таких правил для практичної організації обчислень.

І Похибка суми кількох чисел при розрахунку на ЕОМ зменшиться, якщо починати додавання з менших за величиною доданків.

Якщо додається досить багато чисел, то їх краще розбити на групи з чисел близьких за величиною, провести додавання в групах за вищезгаданою рекомендацією, після чого отримані суми додати, починаючи з меншої.

Якщо задано додатних чисел приблизно однакової величини, то загальна помилка округлення зменшиться, якщо числа додати спочатку групами по n-чисел, а потім додати n – часткових сум. При великих n верхня межа округлення при такому способі становить всього 1/n від відповідної межі при довільному додаванні чисел одне до одного.

Причина того, що не виконується комутативний закон додавання, полягає в округленні проміжних результатів, коли багатозначні числа не вміщуються в розрядну сітку ЕОМ. Тому і не все одно, в якому порядку необхідно виконувати арифметичні операції, щоб результат був якомога точнішим.

ІІ Варто уникати віднімання двох майже однакових чисел. Обчислюючи різницю двох чисел, доцільно винести за дужки їхній спільний множник. Для прикладу обчислимо величину

Винесемо число “4” за дужки, одержимо точний результат:

Зменшити похибку різниці дозволяють перетворення:

Тут - мале в порівнянні з a число.

1.6 Машинна арифметика

ВЕОМ для кодування дійсних чисел використовується двійкова система зчислення й прийнята форма подання чисел із плаваючою точкою ,, . Тут - мантиса ; - двійкові цифри, причому завжди =1, p-ціле число, що називається двійковим порядком. Кількість t цифр, що приділяється для запису мантиси, називається розрядністю мантиси. Діапазон подання чисел в ЕОМ обмежений кінцевою розрядністю мантиси й значенням числа p. Усі числа, що подані в ЕОМ, задовольняють нерівності: , де , . Усі числа, за модулем більші , не подані в ЕОМ і розглядаються як машинна нескінченність. Усі числа, за модулем менші , для ЕОМ не відрізняються від нуля й розглядаються як машинний нуль. Машинним іпсилоном називається відносна точність ЕОМ, тобто границя відносної похибки подання чисел в ЕОМ. Покажемо, що . Нехай , тоді границя абсолютної похибки подання цього числа дорівнює . Оскільки 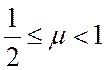, то величина відносної похибки подання оцінюється так:

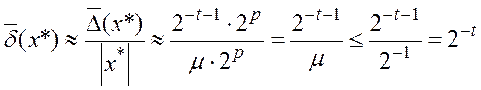Машинний іпсилон визначається розрядністю мантиси та способом округлення чисел, реалізованим на ЕОМ.

Візьмемо такі способи визначення наближених значень параметрів, необхідних у задачі:

1 Покладемо , де n - перше натуральне число, при якому відбувається переповнення.

2 Покладемо , де m – перше натуральне число , при якому збігається з нулем.

3 Покладемо , де k – найбільше натуральне число, при якому сума обчисленого значення 1+ ще більша за 1. Фактично є границя відносної похибки подання числа .