Необхідно скласти план роботи верстатів, щоб витрати були мінімальні.
Керовані змінні ![]() – час,
протягом якого верстат
– час,
протягом якого верстат ![]() зайнятий виготовленням продукції
зайнятий виготовленням продукції
![]() .
.
Область припустимих рішень задається сукупністю систем нерівностей
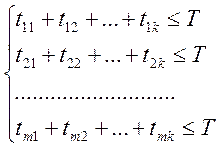 (3.3)
(3.3)
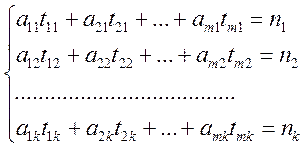 (3.4)
(3.4)
![]() . (3.5)
. (3.5)
Тут (3.3) задає обмеження за часом, (3.4) - необхідне виконання плану за номенклатурою, (3.5) - природні обмеження на керовані змінні.
Функція мети
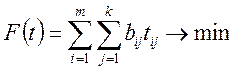 . (3.6)
. (3.6)
Приклад 3.3 Задача проектної оптимізації
Необхідно вибрати співвідношення між
параметрами поперечного перерізу каналу для транспортування води. Вважаємо, що
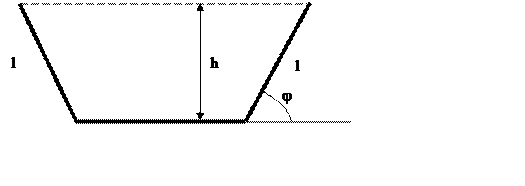
бічні стінки й дно складаються з бетонних плит однакової ширини ![]() . Перерізом каналу є рівнобічна трапеція (рис.
3.1).
. Перерізом каналу є рівнобічна трапеція (рис.
3.1).
 |
|
Рисунок 3.1
1 Визначення меж об'єкта.
У нашому випадку вважаємо, що об'єктом
досліджуваної операції є форма й розміри поперечного перерізу каналу, повністю
обумовлені шириною бетонних плит ![]() і кутом нахилу
і кутом нахилу ![]() . Будемо вважати, що використовуються
стандартні плити шириною
. Будемо вважати, що використовуються
стандартні плити шириною ![]() . Істотною є тільки
пропускна здатність каналу, обумовлена площею поперечного перерізу.
. Істотною є тільки
пропускна здатність каналу, обумовлена площею поперечного перерізу.
2 Керованою змінною в цьому випадку буде ![]() – кут нахилу бічних стінок стосовно
горизонталі.
– кут нахилу бічних стінок стосовно
горизонталі.
3 Область припустимих рішень визначається як
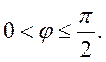 (3.7)
(3.7)
4 Функція мети
![]() , де
, де ![]() – площа поперечного перерізу, а
– площа поперечного перерізу, а ![]() – швидкість течії, що вважається
постійною. Отже,
– швидкість течії, що вважається
постійною. Отже,
![]() (3.8)
(3.8)
Приклад 3.4 Задача про багатоступеневу ракету
За допомогою ![]() –
ступеневої ракети із заданою стартовою масою
–
ступеневої ракети із заданою стартовою масою ![]() запускається
об'єкт маси
запускається
об'єкт маси ![]() . За час роботи кожної ступені ракета
одержує додаткову швидкість
. За час роботи кожної ступені ракета
одержує додаткову швидкість ![]() , де
, де ![]() – маса, що розганяється цією ступенню,
– маса, що розганяється цією ступенню, ![]() – маса самої ступені.
– маса самої ступені.
Знайти такий розподіл загальної маси ракети ![]() між її ступенями, при якому кінцева
швидкість об'єкта буде максимальною.
між її ступенями, при якому кінцева
швидкість об'єкта буде максимальною.
1 Визначення меж об'єкта вибране «ОПР» при змістовній постановці.
2 Керованими змінними будуть:
– ![]() – маса
– маса ![]() -ї
ступені, вважаючи, що стартова маса
-ї
ступені, вважаючи, що стартова маса ![]() , а наприкінці розгону –
, а наприкінці розгону –
![]() ;
;
– ![]() – маса об'єкта разом із пов'язаними з ним
ступенями ракети.
– маса об'єкта разом із пов'язаними з ним
ступенями ракети.
Тоді
![]() ,
, ![]() ,
, ![]() . (3.9)
. (3.9)
3 Область припустимих рішень задається обмеженнями
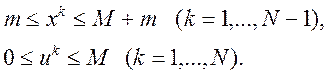 (3.10)
(3.10)
4 Функція мети буде залежати від приросту швидкості на кожному етапі. Кінцева швидкість буде визначатися як
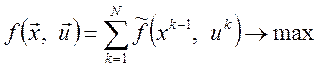 . (3.11)
. (3.11)
Приклад 3.5 Задача матричної гри
Задано матрицю чисел
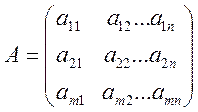 .
.
Два гравці одночасно називають по одному
числу: перший гравець називає номер рядка ![]() другий-номер
стовпця j=1,…, m. Число, розташоване на перетині названого рядка й стовпця в матриці
другий-номер
стовпця j=1,…, m. Число, розташоване на перетині названого рядка й стовпця в матриці ![]() – виграш першого гравця, якщо
– виграш першого гравця, якщо ![]() , та виграш другого, якщо
, та виграш другого, якщо ![]() .
.
1 Керованими змінними є номери вибраних рядків
![]() і стовпців
і стовпців ![]() .
.
2 Область припустимих рішень обмежується розмірами матриці
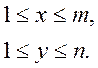 (3.12)
(3.12)
3 Функцією мети є значення вибраного елемента матриці
![]() . (3.13)
. (3.13)
Природно, що розв’язання даної задачі буде відшукуватися у вигляді ймовірнісних характеристик можливості максимального виграшу.
4 Класифікація задач дослідження операцій
Математичні моделі задачі дослідження операцій мають досить різноманітний з погляду математичних методів вигляд. Для того щоб виробити однаковий підхід до їх розв’язання, необхідно їх класифікувати:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.