Методичні вказівки та контрольні завдання з теми «Основні поняття дослідження операцій» курсу «Методи оптимізації та дослідження операцій», страница 2

У практиці дослідження операцій необхідно, наскільки це можливо, спрощувати процеси, що підлягають дослідженню, розділяючи складні системи на більш прості підсистеми, якщо це вплине на остаточний результат у припустимих межах.

2.2 Вибір керованих змінних

На цьому етапі створення математичної моделі необхідно провести розподіл між величинами, значення яких можна змінювати (варіювати) і вибирати їх значення з деякої області з метою досягнення екстремуму функції мети, і величинами, які фіксовані або визначаються зовнішніми факторами.

Величини, що варіюються і впливають на значення функції мети, називаються керованими змінними.

Знаходження значень керованих змінних, яким відповідає екстремальне значення функції мети, і є оптимальним рішенням задачі дослідження операцій.

Зазначимо, що ті самі величини залежно від вибраних меж об'єкта дослідження й рівня адекватності моделі можуть бути керованими чи ні.

2.3 Область припустимих рішень

При створенні математичної моделі на область зміни керованих змінних, як правило, накладаються обмеження, пов'язані з реальними відповідностями змінних соціальним, фізичним, технічним або економічним характеристиками. У математичній моделі ці обмеження записуються у вигляді сукупності нерівностей і рівностей або вказуються множини, яким повинні належати значення керованих змінних. Елементи множини, що задовольняють відповідним обмеженням, утворюють область припустимих рішень  відповідної задачі.

2.4 Функція мети

Обов'язковою складовою частиною математичної моделі є критерій ефективності, мінімальному або максимальному значенню якого відповідає рішення задачі дослідження операцій. Такий критерій повністю визначається вибраними значеннями керованих змінних з області припустимих рішень і називається функцією мети.

У конкретних задачах дослідження операцій функцією мети може бути час обробки інформації у комп'ютерній мережі, споживана енергія в технологічному процесі, прибуток у банківській справі, калорійність дієти і т. ін.

Вибір функції мети є далеко неочевидним. Залежно від конкретної ситуації з багатьох критеріїв вибирають основний, нехтуючи іншими, або будують комплексний критерій, тобто функцію мети, що містить у собі з розумно вибраними ваговими коефіцієнтами критерії, що відповідають різним цілям.

2.5 Формулювання задачі дослідження операції

Поєднуючи все сказане про побудову математичної моделі, задачі дослідження операції можна в досить загальному вигляді сформулювати так: знайти екстремум (мінімум або максимум) функції мети з урахуванням обмежень на керовані змінні. Під мінімізацією (максимізацією) функції мети, що залежить від  змінних  на заданій множині припустимих рішень U(x)  -вимірного простору , будемо розуміти визначення хоча б однієї точки,  у якій  досягає свого екстремуму й обчислення .

Символічно це можна записати як

,

де  – цільова функція.

Зазначимо, що задача мінімізації перетвориться в задачу максимізації, якщо функцію мети помножити на .

3 Приклади побудови математичних моделей задач дослідження операцій

Приклад 3.1 Задача про використання ресурсів

Для виготовлення  видів продукції використовується  видів ресурсів запасу . На виробництво кожного -го виду продукції використовується  одиниць  ресурсу. Кожна одиниця продукції дає  одиниць прибутку. Скласти план виробництва продукції, при якому прибуток буде максимальним.

Керовані змінні  - число одиниць продукції .

Область припустимих рішень буде задана нерівностями

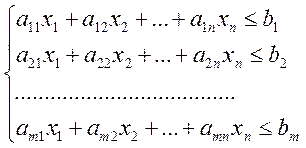                                         (3.1)

і умовою

Функція мети має вигляд

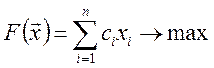                                         .                          (3.2)

Приклад 3.2 Задача про завантаження устаткування

Підприємству заданий план виробництва продукції за часом і номенклатурою: необхідно за час  випустити  одиниць продукції . Продукція виробляється на верстатах . Продуктивність кожного верстата –  ( продукції на  верстаті) і витрати  на виготовлення  продукції на  верстаті в одиницю часу.