Відповіді на тестові запитання і завдання по розділах "Математичні моделі", "Випадкові величини", "Статистичні гіпотези"

Питання і завдання до розділу 1

1 Для чого необхідні математичні моделі.

нахождение  зависимостей и взаимосвязей между ними путем построения математических моделей и последующего их количественного описания позволяет глубже понять существующие закономерности

2 Детерміновані моделі. Наведіть приклад.

Использование детерминированных моделей предполагает, что каждое событие является следствием другого,  и связь между причиной и следствием может быть выражена вполне точно в виде конкретных математических формул. Такая связь называется функциональной. Случайными отклонениями при этом пренебрегают, относя их на счёт ошибок наблюдений и измерений.

Типичными примерами таких зависимостей могут служить законы классической механики.

3 Стохастичні моделі. Їх особливості. Наведіть приклади стохастичних моделей.

В основе стохастических моделей лежит случайный характер величины, оцениваемый вероятностными методами.

Стохастические модели описывают закономерности, обусловленные одновременным действием на объект многих факторов и проявляющихся отчётливо только при массовых наблюдениях.

Такие модели применяются при экономических, медико-биологических, сельскохозяйственных и др. исследованиях, а также для описания технологических процессов в машиностроении и т.д.

4 Предмет математичної статистики. ЇЇ роль у аналізі даних.

Математическая статистика – это наука, занимающаяся методами обработки экспериментальных данных.

Задачи, которые решает математическая статистика:

1) систематизировать полученный статистический материал;

2) на основании полученных экспериментальных данных оценить интересующие нас числовые характеристики наблюдаемой случайной величины;

3) определить число опытов, достаточное для получения достоверных результатов при минимальных ошибках измерения.

Одной из задач третьего типа является задача проверки правдоподобия гипотез.

Таким образом, математическая статистика помогает экспериментатору лучше разобраться в полученных опытных данных, оценить, значимы или нет определенные наблюденные факты, принять или отбросить те или иные гипотезы о природе рассматриваемого явления.

5 Дайте визначення вимірювання.

Измерения – присвоение чисел предметам или событиям, основанное на некоторой системе правил.

6 Шкали вимірювання. Дайте характеристику кожній шкалі.

7 Наведіть приклади для кожного типу шкал.

а) Шкала классификации. Допустимы операции  =, ≠. Нумерация или наименование служат для идентификации объекта (номер дома, номер методики и т.д.).

б) Шкала порядка. Возможны операции сравнения объектов по величине (<. >, =). Пример: шкала твердости минералов, степень тяжести заболевания.
Значения, выставленные разными экспертами, могут не совпадать, поскольку носят субъективный характер. 

в) Шкала интервалов. Возможны не только операции сравнения больше или меньше, но и «на сколько больше» (=, <. >, +, -).

г) Шкала отношений. В этой шкале возможно ответить на  вопрос «во сколько раз больше (меньше)» значение величины. (=, ≠, <. >, +, -, *, /)

Питання і завдання до розділу 2

1 Дайте визначення випадкової величини.

Случайной называется величина, которая в результате эксперимента может принимать неизвестное заранее  значение.

2 Дискретні випадкові величини. Наведіть приклади дискретних випадкових величин.

Дискретной случайной называется величина, которая принимает отдельные значения (например, количество родившихся детей).

3 Неперервні випадкові величини. Наведіть приклади неперервних випадкових величин.

Непрерывной является величина, возможные значения которой непрерывно заполняют какой-либо интервал (например, масса тела новорожденного).

4. Дайте визначення закону розподілу.

Закон распределения – соответствие между значениями случайной величины и вероятностями их  реализации.

5 У якому вигляді може бути поданий закон розподілу для дискретної випадкової величини?

Закон распределенияможет быть задан в виде таблицы, формулы  или графика.

6 Функція розподілу. ЇЇ властивості.

Функция распределения – это функция F(x), которая задает вероятность того, что случайная величина X в испытании примет значение меньшее, чем заданное х. F(x)=P(X<x).

1.F(x) – неубывающая функция. a > b → F(a) ≥ F(b).

2.F(-¥)=0; F(+¥)=1.

3.Вероятность того, что XÎ(a, b)    P(a ≤ x < b) = F(b) – F(a).

7 Функція щільності розподілу. ЇЇ властивості.

F(x) =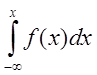 ;  f(x)=F¢(x).

8 Математичне сподівання. Визначення. Формули обчислень для дискретних та неперервних випадкових величин. Що характеризує математичне сподівання?

 M (x) =  Х_i P_i 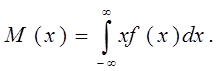    При  k → ∞  М(x) При большом количестве испытаний математическое ожидание приближенно равно среднему арифметическому значению.

9. Дисперсія. Визначення. Формули обчислень для дискретних та непевних випадкових величин. Що характеризує дисперсія?