Асимметрией теоретического распределения называют величину As=М3/σ3
Длинная часть кривой справа As>0.
Длинная часть кривой слева As<0.
9 Що характеризує ексцес?
Для оценки «крутости», то есть большего или меньшего подъема теоретического распределения по сравнению с нормальной кривой пользуются характеристикой – эксцесс.
Эксцесс теоретического распределения:
Ek=(M4/σ4)-3
10 Дайте визначення розподілу Пірсона. Функції Excel для роботи з цим розподілом.
Распределение χ2 имеет случайная величина, представляющая собой сумму квадратов случайных величин, каждая из которых подчиняется стандартному нормальному закону распределения.
χ2 =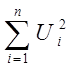
P(χ2>χ2a)=a
XU2PACП(χ; степени свободы) – возвращает вероятность.
XU2ОБP(вероятность; степени свободы) – возвращает значение χ.
11 Дайте визначення розподілу Стьюдента. Функції Excel для роботи з цим розподілом.
Предположим U~N(0,1) не зависит от переменной χ такой, что χ2 имеет χ2-распределителей с n степеней свободы. Тогда распределение переменной
t=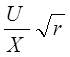 t=
t=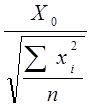
называется распределением Стьюдента с r степенями свободы.
СТЬЮДРАСП (t, степень свободы, признак) – t – значение, для которого вычисляется распределитель Стьюдента.
признак – 1 – для одностороннего распределителя
2 – для двустороннего.
Возвращает вероятность
СТЬЮДРАСПОБР (вероятность, степень свободы)–возвращает значение t.
Если нужно вычислить P(t<ta)=g
СТЬЮДРАСПОБР (1-g, степень свободы)
12 Дайте визначення розподілу Фішера. Функції Excel для роботи з цим розподілом.
Пусть две случайные величины χ12 и χ22 имеют χ2-распределителей с r1 и r2 степенями свободы соответственно. Распределение величин.
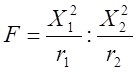 называют F-распределителями с r1 и r2
степенями свободы
называют F-распределителями с r1 и r2
степенями свободы
FРАСП (F; степень свободы 1; степень свободы 2) – вычисляется значение функции.
FРАСПОБР (вероятность; степень свободы 1; степень свободы 2) – вычисляется значение F, которое можно использовать вместо таблиц.
1 Теорема Чебишева.
Если ![]() попарно независимые случайные величины,
причем дисперсии их равномерно ограничена (т.е. не превышают некоторое число
С), то как бы мало не было
попарно независимые случайные величины,
причем дисперсии их равномерно ограничена (т.е. не превышают некоторое число
С), то как бы мало не было ![]() вероятность
неравенства.
вероятность
неравенства.
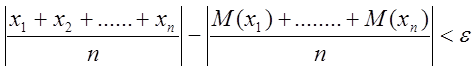
будет как угодно близка к 1, если число случайных величин достаточно велико.
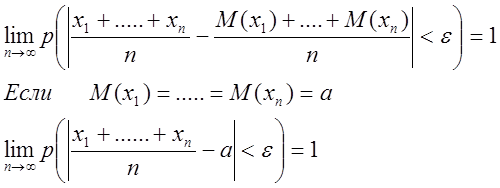
2 Практичне значення теореми Чебишева.
на этой теореме основан широко применяемый в статистике выборочный метод. Суть которого состоит в том, что по сравнительно небольшой выборке судят о всей совокупности исследуемых объектов.
3 Коли застосовується вибірковий метод, його суть.
На практике такое обследование применяется сравнительно редко. Если обследование связано с уничтожением объекта или требует больших материальных затрат, то проводить сплошное обследование не имеет смысла.
В таких случаях из всей совокупности случайно отбирают ограниченное число объектов и подвергают их изучению.
4 Точкові оцінки параметрів розподілу. Їх властивості.
Точечной называют оценку, которая определяется одним числом.
Точечная оценка называется состоятельной, если
![]()
Точечная оценка называется сильно состоятельной, если
![]()
Точечная оценка называется эффективной, если
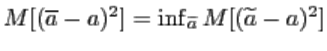 ,
,
где ![]() - все возможные точечные оценки.
- все возможные точечные оценки.
Точечная оценка называется асимптотически эффективной, если
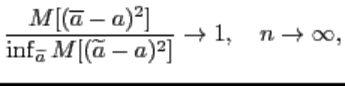
5 Міри положення. Формули для обчислень. Функції Excel.
Среднее
арифметическое (выборочное).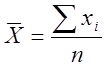 в Excel СРЗНАЧ(<диапазон>)
в Excel СРЗНАЧ(<диапазон>)
Среднее
геометрическое 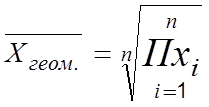 СРГЕОМ
(<диапазон>)
СРГЕОМ
(<диапазон>)
Среднее
гармоническое 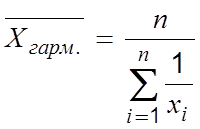 СРГАРМ
(<диапазон>)
СРГАРМ
(<диапазон>)
Мода m0 – МОДА (<диапазон>) Значение, которое наблюдается наибольшее число раз.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.