3 Які гіпотези називають основною та альтернативною?
Нулевой (основной) гипотезой называют выдвинутую гипотезу Н0. Вместе с нулевой гипотезой Н0 выдвигается альтернативная или конкурирующая гипотеза Н1 , которая противоречит нулевой.
4 Який зміст рівня значущості α?
Вероятность α – называют уровнем значимости. Это вероятность совершения ошибки первого рода, то есть отвержение гипотезы Н0, когда она верна.
5 Від чого залежить вигляд критичної області?
Как видим, вид критической области зависит от того, какая гипотеза выдвинута в качестве конкурирующей.
6 Дайте визначення критичної точки.
7 Помилки першого та другого роду. Потужність критерію.
ошибки первого рода, то есть отвержение гипотезы Н0, когда она верна.
Принятие неверной гипотезы называется ошибкой второго рода
8 Вказати порядок дій при перевірці гіпотез.
9 Критерій для перевірки гіпотези про закон розподілу.
Критерієм згоди називають статистичний критерій перевірки гіпотези про передбачуваний закон невідомого розподілу. Він використовується для перевірки згоди передбачуваного виду розподілу з досліджуваними даними на підставі вибірки.
Існують різні критерії згоди: Пірсона, Колмогорова, Фішера, Смирнова та ін.
Критерій згоди Пірсона – найбільш часто вживаний критерій для перевірки гіпотези про закон розподілу.
Критерій
згоди Пірсона - c2 р= 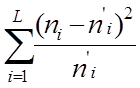 ,
,
Критерій
Фішера - 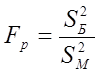 >1,
>1,
10 Критерій для перевірки гіпотез про рівність дисперсій двох нормальних сукупностей. Можливості Excel.
За критерій перевірки нульової гіпотези про рівність двох дисперсій обирається відношення більшої виправленої дисперсії до меншої
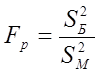 >1,
>1,
що підлягає розподілу Фішера з k1=N1-1; k2=N2-1 ступенями вільності, де N1 і N2 – розміри вибірок.
В Excel: функція FРАСПОБР(a; k;, k2) – повертає Fкр.однобічне.
Пакет Анализ данных: Сервис – Анализ данных – Двухвыборочный F-тест для дисперсии.
11 Критерії для перевірки гіпотез про рівність середніх двох нормальних сукупностей. Можливості Excel.
Можливі такі постановки задач:
1. Порівняння показників контрольної і експериментальної вибірок. Можливі такі випадки:
· вибірки невеликого обсягу (n<30):
- дисперсії вибірок рівні;
- дисперсії вибірок не рівні;
· без припущення про дисперсії (вибірки великі n>30);
2. Порівняння показників вибірки до і після експерименту. У цьому випадку ми маємо справу з так званими зв'язними вибірками.
3. Чи можна вважати, що деяке значення показника дорівнює деякому нормальному значенню.
Перевірка гіпотези про рівність середніх при рівних дисперсіях (малі вибірки n<30)
Використовується критерій Стьюдента :
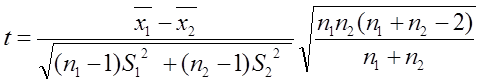
з k=n1+n2-2 ступенями вільності,
де
![]() обсяг вибірок;
обсяг вибірок;
![]() середні значення;
середні значення;
![]() виправлені дисперсії.
виправлені дисперсії.
Використання пакета аналізу значно спрощує розрахунки. Обираємо в меню Сервис – Анализ данных – Двухвыборочный t – тест с одинаковыми дисперсиями.
Перевірка гіпотези про рівність середніх при нерівних дисперсіях (малі вибірки)
Використовується критерій Стьюдента
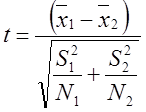 ,
,
В Excel Сервис – Анализ данных – Двухвыборочный t-тест с разными дисперсиями.
Перевірка гіпотез про середні з довільно розподіленими дисперсіями (вибірки великі n >30, незалежні)
Критерій
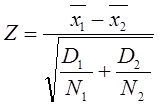 ,
,
де D1та
D2 – дисперсії вибірок; ![]() розміри вибірок;
розміри вибірок;
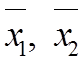 – середні значення вибірок.
– середні значення вибірок.
Вибираємо в пакеті Анализ данных – Двухвыборочный Z–тест для средних.
Перевірка гіпотези про рівність середніх при зв'язаних вибірках
Критеріальне значення обчислюється за формулою
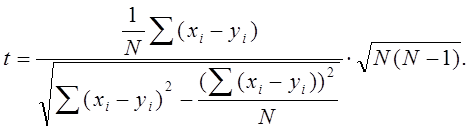
Пакет Анализ данных–Парный двухвыборочный t-тест для средних.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.