Пусть дана последовательность
чисел ![]() , определим
, определим 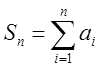 . Для любого
. Для любого ![]() можно получить последовательность
можно получить последовательность ![]() . Если последовательность
. Если последовательность ![]() имеет предел, равный
имеет предел, равный ![]() :
: ![]() , то это можно обозначить следующим
образом
, то это можно обозначить следующим
образом 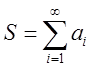 . Тогда
. Тогда 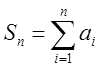 называется частной суммой ряда,
а формула
называется частной суммой ряда,
а формула 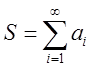 называется числовым
рядом. В этом случае последовательность
называется числовым
рядом. В этом случае последовательность ![]() - это последовательность частичных
сумм. Конечный или бесконечный предел
- это последовательность частичных
сумм. Конечный или бесконечный предел ![]() частичных
сумм
частичных
сумм ![]() ,
, ![]() называется суммой ряда. Если
ряд имеет конечную сумм, то его называют сходящимся, в противном случае
(если сумма ряда равна
называется суммой ряда. Если
ряд имеет конечную сумм, то его называют сходящимся, в противном случае
(если сумма ряда равна ![]() )
ряд называют расходящимся.
)
ряд называют расходящимся.
Если в 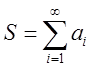 отбросить первые
отбросить первые ![]() членов, то мы получим ряд
членов, то мы получим ряд 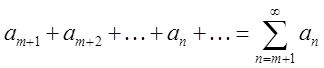 . Эта сумма называется остатком
ряда после отбрасывания первых
. Эта сумма называется остатком
ряда после отбрасывания первых ![]() членов.
членов.
Свойства: 1. Если сходится ряд,
то сходится любой из его остатков. Из сходимости остатка следует сходимость
ряда. Замечание: Отбрасывание конечного числа первых членов ряда или
присоединение в начало ряда нескольких новых членов не отражается на поведении
ряда, т.е. его сходимости или расходимости. 2. Если ряд сходится, то сумма ![]() его остатка после m-ого
члена
его остатка после m-ого
члена ![]() . 3. Если
сходится ряд, то ряд вида
. 3. Если
сходится ряд, то ряд вида 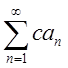 тоже
сходится. 4. Два сходящихся ряда
тоже
сходится. 4. Два сходящихся ряда 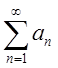 и
и
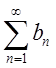 можно почленно складывать
и вычитать:
можно почленно складывать
и вычитать: 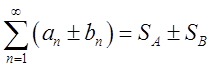 . 5. Общий член
ряда
. 5. Общий член
ряда ![]() . Замечание: Свойство 5 – необходимое
условие сходимости ряда. При нарушении этого условия ряд заведомо
расходится. Это условие не является достаточным.
. Замечание: Свойство 5 – необходимое
условие сходимости ряда. При нарушении этого условия ряд заведомо
расходится. Это условие не является достаточным.
Ряд, составленный из ![]() , называется положительным.
Тогда
, называется положительным.
Тогда ![]() , т.е. частичная
сумма будет возрастающей. Сумма положительного ряда будет конечной, и
ряд будет сходиться в случае, когда частичная сумма ряда ограничена сверху, в
обратном случае – бесконечной.
, т.е. частичная
сумма будет возрастающей. Сумма положительного ряда будет конечной, и
ряд будет сходиться в случае, когда частичная сумма ряда ограничена сверху, в
обратном случае – бесконечной.
Ряд вида 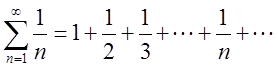 , называется гармоническим.
Частичные суммы гармонического ряда нельзя ограничить сверху, т.е. ряд будет
расходиться. Ряд вида
, называется гармоническим.
Частичные суммы гармонического ряда нельзя ограничить сверху, т.е. ряд будет
расходиться. Ряд вида 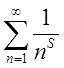 называется
гармоническим рядом (
называется
гармоническим рядом (![]() - гармоническое
число). Этот ряд также расходится при любом
- гармоническое
число). Этот ряд также расходится при любом ![]()
Теоремы сравнения. 1.
Пусть даны два положительных ряда 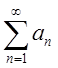 и
и
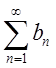 . Если
. Если ![]() , то из сходимости ряда
, то из сходимости ряда ![]() следует сходимость ряда
следует сходимость ряда ![]() . А из расходимости ряда
. А из расходимости ряда ![]() следует расходимость ряда
следует расходимость ряда ![]() . 2. Если существует
. 2. Если существует 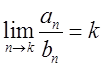 , где
, где ![]() , то из сходимости ряда
, то из сходимости ряда ![]() следует сходимость ряда
следует сходимость ряда ![]() , если
, если ![]() . А из расходимости ряда
. А из расходимости ряда ![]() следует расходимость ряда
следует расходимость ряда ![]() , если
, если ![]() . Т.е.
если
. Т.е.
если ![]() , то оба ряда сходятся и
расходятся одновременно. 3. Если, начиная с некоторого
, то оба ряда сходятся и
расходятся одновременно. 3. Если, начиная с некоторого 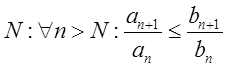 , то из сходимости ряда
, то из сходимости ряда ![]() следует сходимость ряда
следует сходимость ряда ![]() , а из расходимости ряда
, а из расходимости ряда ![]() следует расходимость ряда
следует расходимость ряда ![]() (сверху ограничивают сходящимся
рядом, если хотят доказать сходимость; снизу ограничивают расходящимся, если
хотят доказать расходимость).
(сверху ограничивают сходящимся
рядом, если хотят доказать сходимость; снизу ограничивают расходящимся, если
хотят доказать расходимость).
Признак Коши. Пусть дан
ряд ![]() , рассмотрим
, рассмотрим ![]() , если для достаточно больших
, если для достаточно больших ![]() выполняется
выполняется ![]() , то ряд сходится. Если же, начиная
с некоторого
, то ряд сходится. Если же, начиная
с некоторого ![]() ,
, ![]() , то ряд, составленный из
, то ряд, составленный из ![]() расходится. Предельный признак
Коши. Если существует
расходится. Предельный признак
Коши. Если существует ![]() ,
тогда при
,
тогда при ![]() ряд сходится, а
при
ряд сходится, а
при ![]() ряд расходится.
ряд расходится.
Признак Даламбера. Для
ряда ![]() рассмотрим величину
рассмотрим величину 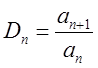 . Если при достаточно больших
. Если при достаточно больших ![]() , то ряд сходится, если же с
некоторого
, то ряд сходится, если же с
некоторого ![]() , то ряд
расходится. Предельный признак Даламбера. Если существует
, то ряд
расходится. Предельный признак Даламбера. Если существует ![]() , тогда при
, тогда при ![]() ряд сходится, при
ряд сходится, при ![]() ряд расходится.
ряд расходится.
Замечания: 1. Признак Даламбера
не работает при ![]() . 2. Признак Коши
сильнее признака Даламбера. 3. Если признаки Коши и Даламбера не дают точного
ответа, то можно воспользоваться сравнением ряда
. 2. Признак Коши
сильнее признака Даламбера. 3. Если признаки Коши и Даламбера не дают точного
ответа, то можно воспользоваться сравнением ряда ![]() с известным гармоническим рядом.
с известным гармоническим рядом.
Признак Раабе. Если при
достаточно больших ![]() , где
, где 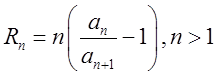 , то ряд
, то ряд ![]() сходится, если же
сходится, если же ![]() , то ряд расходится. Замечания: 4.
Признак Раабе сильнее признака Даламбера. 5. При
, то ряд расходится. Замечания: 4.
Признак Раабе сильнее признака Даламбера. 5. При ![]() признак Раабе не работает, где
признак Раабе не работает, где ![]() .
.
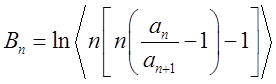 . Если существует
. Если существует Предельным рядом называется ряд, члены которого могут иметь различные знаки.
Критерий Коши. Для
сходимости ряда ![]() необходимо и
достаточно, чтобы
необходимо и
достаточно, чтобы 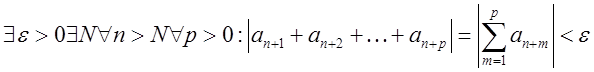 . Ряд будет
расходится, если
. Ряд будет
расходится, если 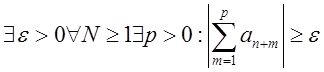 .
.
Теорема. Если сходится
ряд, составленный из ![]() ,
то ряд, составленный из
,
то ряд, составленный из ![]() ,
тоже сходится (Следствие из критерия Коши). Если ряд
,
тоже сходится (Следствие из критерия Коши). Если ряд ![]() сходится вместе с рядом
сходится вместе с рядом ![]() , то такой ряд называется абсолютно
сходящимся. Если же ряд
, то такой ряд называется абсолютно
сходящимся. Если же ряд ![]() сходится,
а ряд, составленный из
сходится,
а ряд, составленный из ![]() не
сходится, то ряд
не
сходится, то ряд ![]() называется условно
(не абсолютно) сходящимся. Замечание: Для абсолютно сходящихся
рядов применим признак Даламбера.
называется условно
(не абсолютно) сходящимся. Замечание: Для абсолютно сходящихся
рядов применим признак Даламбера.
Если ряд можно записать в виде 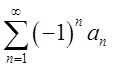 , то такой ряд называется знакопеременным
(знакочередующимся).
, то такой ряд называется знакопеременным
(знакочередующимся).
Теорема Лейбница. Если
члены знакопеременного ряда монотонно убывают по модулю (![]() ) и
) и ![]() , то ряд будет сходиться. Ряд
Лейбница:
, то ряд будет сходиться. Ряд
Лейбница: 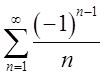 .
.
Если 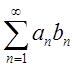 , где
, где ![]() - последовательности вещественных
чисел, то:
- последовательности вещественных
чисел, то:
Признак Абеля. Если ряд ![]() сходится, числа
сходится, числа ![]() образуют монотонную и ограниченную
последовательность
образуют монотонную и ограниченную
последовательность ![]() , тогда ряд сходится.
Признак Дирихле. Если частные суммы ряда
, тогда ряд сходится.
Признак Дирихле. Если частные суммы ряда ![]() в совокупности ограничены
в совокупности ограничены ![]() , а числа
, а числа ![]() образуют монотонную
последовательность, стремящуюся к нулю (
образуют монотонную
последовательность, стремящуюся к нулю (![]() ), то ряд сходится. Замечание:
Признак Абеля вытекает из признака Дирихле.
), то ряд сходится. Замечание:
Признак Абеля вытекает из признака Дирихле.
Сочетательное свойство
сходящихся рядов. Если члены сходящегося ряда ![]() объединить произвольным образом в
две группы:
объединить произвольным образом в
две группы: ![]() , тогда если
последовательность индексов
, тогда если
последовательность индексов ![]() - это
возрастающая последовательность, то новый ряд тоже будет сходиться и иметь ту
же сумму, что и ряд
- это
возрастающая последовательность, то новый ряд тоже будет сходиться и иметь ту
же сумму, что и ряд ![]() . Переместительное свойство. Пусть дан сходящийся ряд,
сумма которого равна
. Переместительное свойство. Пусть дан сходящийся ряд,
сумма которого равна ![]() .
Произвольным образом переставив члены этого ряда, мы получим новый ряд
.
Произвольным образом переставив члены этого ряда, мы получим новый ряд ![]() . Если ряд
. Если ряд ![]() сходился, то и ряд
сходился, то и ряд ![]() тоже будет сходиться, и его сумма
будет равна
тоже будет сходиться, и его сумма
будет равна ![]() . Абсолютно
сходящийся ряд обладает переместительным свойством. Умножение рядов.
Если оба ряда
. Абсолютно
сходящийся ряд обладает переместительным свойством. Умножение рядов.
Если оба ряда 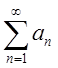 и
и 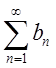 сходятся абсолютно, то произведение
этих двух рядов может быть построено по правилу бесконечной матрицы:
сходятся абсолютно, то произведение
этих двух рядов может быть построено по правилу бесконечной матрицы: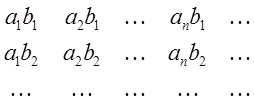 . Сумма этого ряда будет
сходиться, и произведение этих рядов будет равно
. Сумма этого ряда будет
сходиться, и произведение этих рядов будет равно ![]() .
.
Двойной ряд – это ряд вида
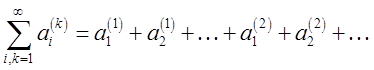 . Если этот ряд имеет
конечную сумму, то он называется сходящимся.
. Если этот ряд имеет
конечную сумму, то он называется сходящимся.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.