IV. Функциональные ряды.
Пусть
дана последовательность {fn(x)}, определенных на [a;b]. f(x),
определенную на [a;b] называют пределом функциональной последовательности fn(x), если для " x0Î[a;b] 
Рассмотрим ряд, составленный из fn(x). Сумма ряда S(x) =
. Частичная сумма
.
Равномерная сходимость: Функциональная последовательность fn(x) называется равномерно-сходящейся на x Î [a;b] в некоторой функции f(x), если для "ε >0 в последовательности функций $ fN(x), что для " n>N и "x Î [a;b]: |f(x)-fN(x)|<ε.
Свойства равномерно сходящихся последовательностей:
1)Если {fn(x)} и {gn(x)} сходятся к f(x) и g(x), λ и μ – константы, то {λfn(x)+μgn(x)} сходится к λf(x)+μg(x). 2)Если {fn(x)} равномерно сходится, а функция φ(x) ограничена на [a;b], то последовательность {fn(x)φ(x)} будет равномерно сходиться к f(x)φ(x) на этом промежутке.
Теорема о равномерной сходимости:
Для того, чтобы {fn(x)} равномерно сходилась на [a;b] к некоторой f(x) ó " ε>0 $N, который не зависит от х, что "n>N и "p,q>n выполнялось неравенство |fp(x)-fq(x)|<ε "xÎ[a;b] Доказательство: -> Пусть {fn(x)} -> x, выберем ε`>0. Тогда из определения: в последовательности $ fN(x) такая, что |fn(x)-f(x)|<ε`. Выберем две произвольные последовательности {fp(x)},{fq(x)}, p,q>N. И рассмотрим |fp(x)-fq(x)|=|fp(x)-fq(x)+f(x)-f(x)|≤ |fp(x)-f(x)|+|fq(x)-f(x)|≤ε`+ε`=2ε`. Выберем ε`=ε/2. ->доказана.
<- Пусть {fn(x)} удовлетворяет условию |fp(x)-fq(x)|<ε. Тогда она сходится для "х Î[a;b]. Это вытекает из теоремы Коши для последовательностей. Обозначим lim fn(x)=f(x) и пусть ε>0. В силу предположения в последовательности есть такая fN(x), что для "n>N выполняется |fp(x)-fq(x)|<ε. "p,q>n. "xÎ[a;b] или |fp(x)-fn(x)|<ε. Тогда lim(p->∞) |fp(x)-fn(x)|. Получим, что для "n>N: |f(x)-fn(x)|≤ε. Следовательно, fn(x) будет сходиться равномерно.
Теорема. lim{fn(x)} есть непрерывная функция.
Говорят,
что сходится равномерно "xÎ[a;b], если $ {Sn(x)} его
частичных сумм, которая сходится равномерно на [a;b]
Критерий
Коши: Для того, чтобы сходился равномерно на [a;b] ó для "ε>0 $
N, что для "n>N, " m>0 выполнялось: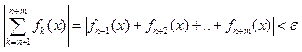
.
Признаки равномерной сходимости:
Вейерштрассе:
Пусть дан ряд (1) и сходящийся числовой ряд
. Если, начиная с некоторого N для "n>N: |fn(x)|≤an на
[a;b], то ряд 1 будет равномерно сходиться на [a;b]. Доказательство:
по сравнению с числовыми рядами и оценке |Sp(x)-Sq(x)|. p,q>N
Абеля:
Пусть дан ряд (2)
, сходящийся равномерно на [a;b], а
функции {an(x)} образуют монотонную последовательность и в
совокупности |an(x)|≤K для "n,xÎ[a;b], k=const.
Тогда ряд (3)
будет равномерно сходиться для "xÎ[a;b]
Дирихле:
Пусть частичная сумма ряда 2 
для "х и n
ограничены. |Sbn(x)|≤M, а функции an(x)
образуют монотонную последовательность, которая на заданном отрезке равномерно
сходится к нулю. Тогда ряд 3 будет равномерно сходиться на [a;b]
Свойства равномерно сходящихся рядов.
Т1. Пусть функции fn(x) определены
на [a;b] и непрерывны в некоторой точке x0Î[a;b]. Если
ряд составленный из fn(x) равномерно сходится для всех хÎ[a;b], то
сумма ряда 
в точке х=х0 также будет
непрерывна.
Т2. Пусть члены ряда fn(x) непрерывны и положительны на всем отрезке [a;b]/ Если сумма ряда S(x) также непрерывна на всем отрезке, то ряд равномерно сходится на всем отрезке [a;b]
Т3. Функция f(x) определена на [b;d] и
имеет конечный предел. Если ряд, составленный из fn на
промежутке [b;d] сходится равномерно, то сходится и ряд, составленный
из lim.
, Тогда при x->a lim S(x)=Sc
Т4. Почленное интегрирование рядов
Если функции fn(x) непрерывны на [a;b] и
соответствующий функциональный ряд сходится на [a;b]
равномерно, то(*):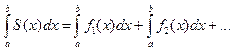
Доказательство: Интегрируем сумму с остатком вида
. Затем доказываем, что ->0, при n->∞ (из
равномерной сходимости фун.ряда)
Т5. Если функции fn(x) интегрируемы на [a;b] и составленный из них ряд сходится равномерно, то S(x) тоже будет интегрируем и имеет место соотношение *.
Т6. Почленное дифференцирование рядов
Пусть fn(x)
определены на [a;b] и имеют на нем непрерывные производные. И пусть на
этом отрезке ряд, составленный из f’n(x)
равномерно сходится. (**)
. Тогда S(x)
имеет на [a;b] производную, причем она равна сумме ряда производных.
Доказательство: Т.к. S*(x) – непрерывная функция - интегрируем ее на [a;x](Т4) Теперь раскрываем интеграл и получаем: S(x)-S(a). Т.к. S(a) – константа, то интеграл равен S(x). Берем производную от левой и правой частей и получаем S`(x).
Степенным рядом называется ряд вида(1):
.
Лемма: Если степенной ряд 1 сходится для некоторого x =
, то он абсолютно сходится для "x: |x|<||
Пусть множество всех {||}сверху ограничено и R=sup{||}. Если некоторое |x|>R, то
ряд расходится. Если |x|<R, то ряд 1 – абсолютно сходится. Для " степенного ряда 1, если только он не всюду расходящийся, то область
сходимости – промежуток от –R до R (R может быть =∞). Внутри него ряд сходится абсолютно. R-радиус
сходимости ряда 1
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
