Функциональные ряды. Свойства равномерно сходящихся рядов, страница 3

Абеля: Пусть дан ряд (2), сходящийся равномерно на [a;b], а функции {a_n(x)} образуют монотонную последовательность и в совокупности |a_n(x)|≤K для "n,xÎ[a;b], k=const. Тогда ряд (3) будет равномерно сходиться для "xÎ[a;b]

Дирихле: Пусть частичная сумма ряда 2  для "х и n ограничены. |S_bn(x)|≤M, а функции a_n(x) образуют монотонную последовательность, которая на заданном отрезке равномерно сходится к нулю. Тогда ряд 3 будет равномерно сходиться на [a;b]

Свойства равномерно сходящихся рядов.

Т1. Пусть функции f_n(x) определены на [a;b] и непрерывны в некоторой точке x₀Î[a;b]. Если ряд составленный из f_n(x) равномерно сходится для всех хÎ[a;b], то сумма ряда  в точке х=х₀ также будет непрерывна.

Т2. Пусть члены ряда f_n(x) непрерывны и положительны на всем отрезке [a;b]/ Если сумма ряда S(x) также непрерывна на всем отрезке, то ряд равномерно сходится на всем отрезке [a;b]

Т3. Функция f(x) определена на [b;d] и имеет конечный предел. Если ряд, составленный из f_n на промежутке [b;d] сходится равномерно, то сходится и ряд, составленный из lim., Тогда при x->a lim S(x)=S_c

Т4. Почленное интегрирование рядов

Если функции f_n(x) непрерывны на [a;b] и соответствующий функциональный ряд сходится на [a;b] равномерно, то(*):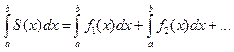

Доказательство: Интегрируем сумму с остатком вида. Затем доказываем, что ->0, при n->∞ (из равномерной сходимости фун.ряда)

Т5. Если функции f_n(x) интегрируемы на [a;b] и составленный из них ряд сходится равномерно, то S(x) тоже будет интегрируем и имеет место соотношение *.

Т6. Почленное дифференцирование рядов

Пусть f_n(x) определены на [a;b] и имеют на нем непрерывные производные. И пусть на этом отрезке ряд, составленный из f’_n(x) равномерно сходится. (**). Тогда S(x) имеет на [a;b] производную, причем она равна сумме ряда производных.

Доказательство:  Т.к. S^*(x) – непрерывная функция - интегрируем ее на [a;x](Т4) Теперь раскрываем интеграл и получаем: S(x)-S(a). Т.к. S(a) – константа, то интеграл равен S(x). Берем производную от левой и правой частей и получаем S`(x).

Степенным рядом  называется ряд вида(1):.

Лемма: Если степенной ряд 1 сходится для некоторого x =, то он абсолютно сходится для "x: |x|<||

Пусть множество всех {||}сверху ограничено и R=sup{||}. Если некоторое |x|>R, то ряд расходится. Если |x|<R, то ряд 1 – абсолютно сходится. Для " степенного ряда 1, если только он не всюду расходящийся, то область сходимости – промежуток от –R до R (R может быть =∞). Внутри него ряд сходится абсолютно. R-радиус сходимости ряда 1

Свойства:

10)  Какое бы r>0, r<R: ряд 1 будет сходиться равномерно относительно х на [-r;r].

11)  Сумма S(x) степенного ряда 1 для " х Î [-R;R] представляет непрерывную функцию. Доказательство из Т1 и свойства 1.

12)  Если 2 степенных ряда в окрестности т. х=0 имеют одну и ту же сумму, то эти два ряда тождественны. Доказательство: положим х=0, затем диф. и положим х=0…

13)  Если в точке х=R степенной ряд 1 расходится, то сходимость степенного ряда на промежутке (0;R) Не может быть равномерной. Доказательство: При равн. сходимости ряда 1 по Т3 можно в соотн. 1 перейти к lim почленно. Т.е. для этого ряд должен сходиться – противоречие.

14)  Если степенной ряд 1 сходится при x=R хотя бы и не абсолютно, тогда $ равномерная сходимость соответствующего функционального ряда 1 на всем промежутке на [0;R]. Доказательство: через умножение, деление на Rⁿ , а потом по Абелю.

15)  Теорема Абеля. Если степенной ряд 1 сходится при х=R, то сумма ряда сохраняет непрерывность и при этом значении х.

16)  Степенной ряд 1  в промежутке [0;x] |x|<R (х из промежутка сходимости) всегда можно проинтегрировать почленно.

17)  Степенной ряд 1 внутри его промежутка сходимости можно дифференцировать почленно.(Т6)

18)  Функция, представленная степенным рядом 1 на его промежутке сходимости имеет внутри этого промежутка производные всех порядков. Сам ряд – ряд Тейлора.

Теорема Коши-Адамара: Радиус сходимости ряда 1 есть величина обратная наибольшему пределу ρ следующих величин:.

Ряд Тейлора: f(x) [x₀;x₀+h], [x₀-h;x₀] h>0 имеет производные всех порядков, которые являются непрерывными функциями. Тогда по свойству 9 она может быть представлена в виде(1). В таком виде – разложение Тейлора r_n – остаточный член. Т.к. r_n может быть сколь угодно большим, его можно заменить на (2)«…». Такой ряд, независимо от того, сходится ли он или нет и имеет ли своей суммой f(x), называется рядом Тейлора для функции f(x).

- коэффициенты Тейлора. Т. к. разность между f(x) и суммой n + 1 члена ряда Тейлора равна r_n., то для того, чтобы при некотором x имело место разложение (2), необходимо и достаточно, чтобы дополнительный член r_n->0 при этом x, при n->∞  . Т.е. при x=0 – ряд Маклорена. Коэффициенты вычисляются по аналогичным формулам.

Остаточные члены в форме Лагранжа: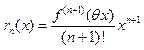

В форме Коши: